벨트구동타입 원심송풍기의 샤프트 피로파괴 및 수치해석 연구
Abstract
In this study, the cause of the fan shaft failure and fatigue failure of S45C steel was analyzed. The fatigue cycle of the broken fan shaft was estimated to be approximately 3.21×106, and the bending stress was estimated through the fracture analysis and ANSYS mechanical structural analysis. FEM analysis of the stress change and displacement of the shaft was performed assuming self-aligning roller bearings and deep groove ball bearings. When self-aligning roller bearings were applied, the deformation increased by approximately 60 %, but the concentrated stress decreased, making the shaft more stable under the load. Additionally, by improving the shaft step radius from 0.5R to 2.5R, a stress reduction effect of approximately 20 to 29% was achieved, depending on the presence or absence of the bearing tilting effect. In addition, excessive belt tension should be sufficiently considered when designing the shaft, and the FEM analysis results show that the ultra-high-cycle fatigue failure of the fan shaft occurred due to a bending load of approximately 4,000∼5,000 N. The newly replaced shaft was found to operate without problems for more than 1.284×109 c ycles b y a djusting t he b elt t ension a nd s haft s tep radius.
Keywords:
Rotating shaft, Structural analysis, Belt tension, Breakage analysis, Fatigue breakage키워드:
회전축, 구조해석, 벨트장력, 파손분석, 피로 파손1. 서 론
송풍기는 현대화된 산업사회에서 환기 및 공기순환을 위해 적용되는 필수 유체기계이다. 우리나라에도 1960년대 이후 많은 송풍기 업체가 생겨나고 신뢰성 있는 성능 및 가격 경쟁력을 갖추기 위하여 많은 연구와 실증이 이루어져 왔다.
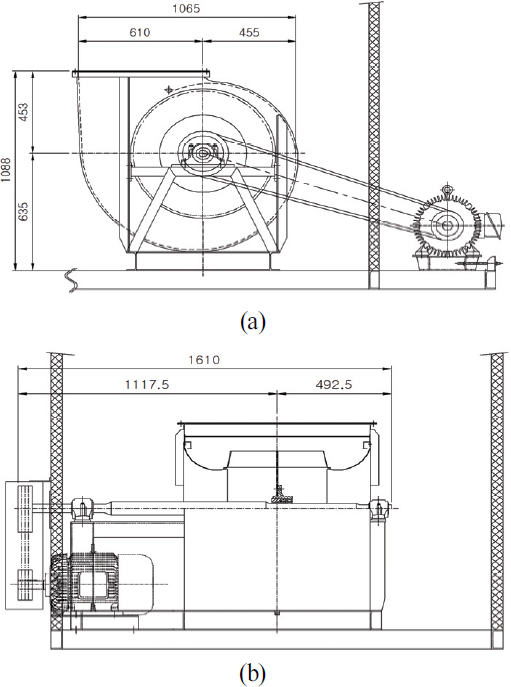
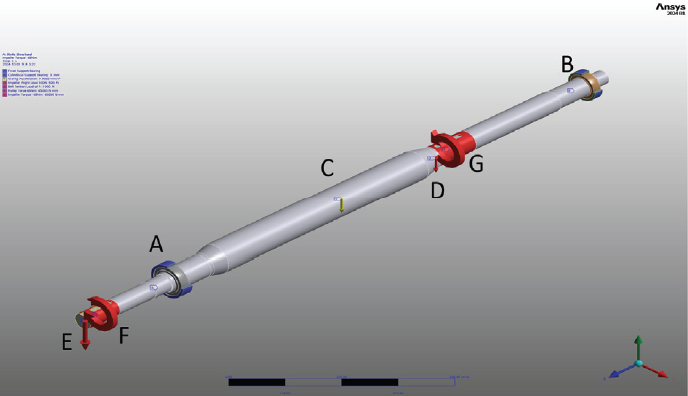
근래에 들어 공기조화기 제조업체들은 보다 저렴한 송풍기 및 부품을 수급하기 위하여 스크롤 하우징이 없는 플레넘 송풍기(Plenum Fan)를 구입하여 적용하거나 송풍기 제조사에 모터 및 벨트, 풀리 등을 제외한 송풍기 기본구성 요소(Bare Shaft Fan)만을 구입하여 자체적인 설계를 진행하여 회전수 및 벨트, 모터 등을 설치하여 적용하는 사례가 점차 증가하고 있다. 아래의 Fig. 1의 (a) 와 (b)는 근래에 사용량이 증가되고 플레넘 송풍기와 있는 양흡입 기본구성 송풍기의 전형적인 사진이다.
외장형 공조기는 송풍기만 내부에 설치하고 모터 및 벨트는 공조기 외부로 배치하여 고무벨트의 슬립에 의한 분진발생을 공조구역과 분리하는 방안으로 적용되었다. 이러한 경우 송풍기의 회전축은 내장형 송풍기에 비해 상당히 길어지게 되어 축의 처짐 및 굽힘 모멘트에 대한 고려가 필요하다.
1.1 연구목적
송풍기의 회전축은 동력전달에 따른 비틀림 응력과 임펠러 중량 및 회전축 자중, 벨트장력에 따른 굽힘 모멘트가 적용된다. 회전축의 직경은 축의 작용하중에 따라 아래의 식에 따라 직경을 결정하고 설계자의 의도에 따라 안전율을 추가하게 된다.
| (1) |
| (2) |
여기에서, Te는 등가 비틀림 응력이고 Me는 등가 굽힘 모멘트이다.
송풍기의 일반적인 손상 형태는 베어링의 내⋅외륜 결함에 따른 진동, 소음 문제가 가장 흔하게 발생되는 문제이며 고속의 임펠러에서 원심력에 의한 블레이드와 주판의 결합부에 균열 또는 절손이 나타나기도 한다. 일부의 경우 축계의 파손이 관찰되기기 때문에 본 연구에서는 샤프트의 파손과 관련하여 벨트의 장력에 의한 피로손상의 형태와 벨트장력의 적정수준을 파악하여 샤프트 설계 개선을 위하여 진행하게 되었다.
1.2 선행연구
Kim1)등은 SAE10B38M2 재질의 차량용 구동 회전축의 비틀림 하중에 대한 피로파괴 개선을 위하여 9개의 형상변수를 설정하고 실험계획법 기반 직교 배열 표를 이용한 설계영역 탐색과 민감도 분석 그리고 크리깅 근사모델을 이용한 형상최적설계를 진행하였으며 최대전단응력 11.5% 감소 및 피로수명 3.7배 증가와 약 25%의 중량감소 효과를 발표하였다. Oh2)는 기계저널의 기고에서 구조물의 무한수명은 106∼107s사이클로 정의되어왔다고 말하였으며 105사이클 미만은 저주기 피로(Low Cycle Fatigue) 그 이상을 고주기 피로(High Cycle Fatigue)로 칭하였다. 또한 108사이클 이상을 초고주기 피로(Very High Cycle Fatigue)로 구분하였으며 초고주기피로영역에서의 응력크기가 상대적으로 낮아 균열발생수명이 전체수명의 99% 이상을 차지한다고 하였다. Yang3) 등은 기계식 프레스의 AISI 4340 강철 크랭크 샤프트내부 주축이 8.9x106사이클에서 파손된 사례를 연구하였으며 개선설계를 통하여 피로수명이 2.5x107사이클이 가능하도록 하였다. Suh4) 등은 SCMH2재질의 표면침탄처리를 실시하는 경우와 실시하지 않은 재료의 충격 시험 및 피로시험을 진행하여 침탄 처리를 하는 경우 충격값은 침탄을 실시하지 않은 충격값의 약 37% 정도로 감소하고 경도는 200.8 Hv에서 756Hv로 약 376.5%로 증가하며 109사이클의 초고주기 피로는 138% 정도 증가한다고 하였다. Jin5) 등은 원자력 발전소의 터빈-발전기 시스템에 적용된 SM 45C 재질의 터빈 축에 대하여 가변 비틀림 응력을 인가하고 이를 Modified Goodman 수식을 이용하여 등가응력으로 변환하여 적용하였으며 등가응력의 증가에 따라 누적손상지수가 지속적으로 증가한다고 하였다. Kim6) 등은 지게차 동력전달 축에 적용되는 프로펠러 샤프트의 교정가속수명시험 방법(Calibrated Accelerated Life Test, CALT)을 시행하였으며 실제 차량의 부하 데이터를 측정하여 피로손상 정도를 정량화하여 누적손실을 고려하는 방법으로 가속수명지수를 적용하였다.
2. 샤프트 파손 송풍기의 주요내역
2.1 공기조화기 내부 설치상태
아래 Fig. 2는 각각 공조기 내부의 송풍기 설치상태의 정면도와 우측면도 이다. 공기조화기 내부에 설치되고 샤프트는 패널 외부로 돌출되어 종동 풀리가 장착되고 V벨트를 통하여 모터 축 구동 풀리와 동력을 전달하는 방식으로 구성되어 있다.
설치된 벨트는 B형 4가닥이 적용되어 있었고 파손당시의 벨트 장력 상태 및 정렬상태는 측정할 수 없었다. 신품 샤프트 교체 시 벨트 장력이 과도하다고 판단되어 모터의 위치를 조정하고 벨트를 신품으로 교체하였다. 설치된 송풍기는 특수 공정이 진행되는 공간의 환기 및 온도 유지를 위한 설비로 활용되었으며 2021년 6월 초 설치 이후 12월 중순까지 약 5.5개월간 가동 후 파손되었다. 특수공정용으로 일평균 20시간 가동상태를 유지하였으며 설계된 송풍기의 회전수는 1,621 rpm이었다. 따라서 송풍기 샤프트에 가해진 하중 사이클을 계산하면 약 3.21×108 회전 정도가 운전된 것으로 추정된다.
2.2 주축의 재질 및 설치상태
설계된 주축의 재질은 기계구조용 탄소강(SM45C)으로 KS D 3752규격7)의 재질이며 규격상 주요 성분의 함량과 실제작품의 화학성분 분석 결과는 아래의 Table 1과 같다.
화학성분 분석은 ASTM E415규격에 따라 시험하였으며 인장강도 및 충격시험은 각각 ASTM E8M과 ASTM E23 규격에 따라 시험을 진행하였다. 화학성분 분석 및 인장강도 시험 및 충격시험, 미세조직 분석은 한국 재료시험 연구원에 파손된 샤프트를 송부하여 시험된 결과이고 결과 값은 Table 2와 같다8).
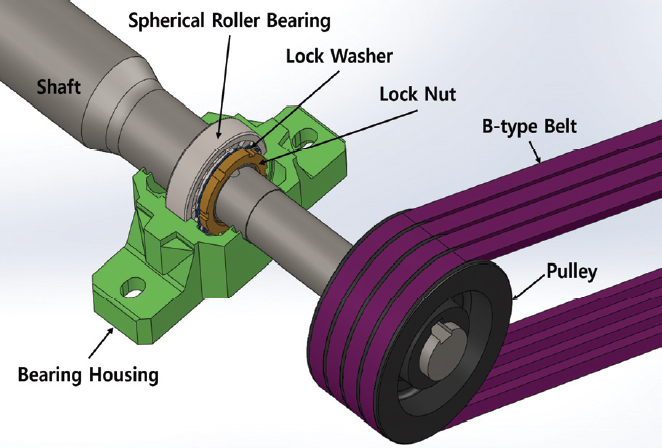
주축의 양측은 구면 자동 조심 롤러 베어링(Spherical Self Aligning Roller Bearing)으로 지지되어 있으며 각각 부하측은 22211와 22209 타입9)이며, 베어링 내경은 원통 구멍타입으로 조립의 원활함을 위하여 약 80℃ 정도로 유도가열 후 주축과 조립하여 풀림방지용 혀붙이 와셔(AW11 및 AW09)와 로크너트(AN11 및 AN09)로 체결하였다.
동력을 전달하는 구동 부품의 설치상태는 다음 Fig. 3과 같이 조립되어 있었다.
Table 3은 충격시험 및 경도시험의 결과이다.
Table 1에서 Table 3까지의 결과를 KS D 3752 : 2019『기계 구조용 탄소 강재』의 참고 값과 비교했을 때 재질은 SM45C의 노멀라이징(Normalizing) 상태의 값을 상회하고 있어 재질상의 문제는 아닌 것으로 판단된다. 판단 기준으로 선정한 KS D 3752의 기준 값은 Table 4에 명기되어있다.
2.3 주축의 파단면 및 파단위치
주축의 파단위치 및 파단면의 형상은 다음의 Fig. 4와 같다. 부하 측 베어링의 M55 나사부위와 Ø50 축 단차부의 위치에서 파손되었으며 축 길이방향에 수직한 단면으로 매우 균일한 단면으로 파손되었다. 초기 원인 추정 시 재질상의 결함으로 추정하였다. 재질상의 문제(설계상의 재질과 실제 재질과의 차이 발생) 또는 초기 내부 결함(내부 균열 발생, 슬러그 혼입 또는 기공포함)으로 추정하였다.
그러나 재질의 화학적 성분검사 결과 SM45C 화학성분과 일치하고 인장강도 시험결과 KS규격의 기준 값을 상회하는 것으로 나타났으며 한국재료연구원의 파단면 육안확인 후 내부적 결함보다는 외부적 하중에 의한 파단으로 추정8)에 따라 추가적인 원인분석을 진행하게 되었다.
3. 외력에 의한 파손원인 파악
3.1 송풍기 주축 형상 및 모델링
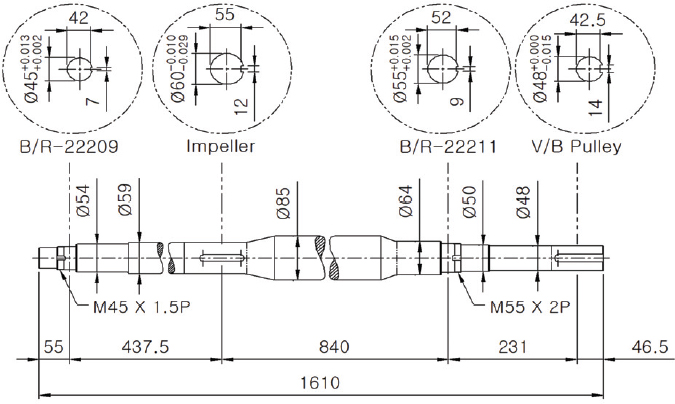
양 흡입 에어포일(Airfoil) 송풍기의 주축은 아래 Fig. 5와 같은 형상과 치수를 가지도록 설계되었다.
송풍기 샤프트의 형상은 SOLIDWORKS 2024 SP 1.0버전으로 3D 모델링하였으며 로크너트 및 나사부분은 모델링에서 제외하였다.
일반적으로 연성재질의 철강재에 적용하는 Von Mises 주응력 수식은 아래와 같다.
| (3) |
상기 Fig. 5의 베어링 중심으로부터 축의 풀리 조립부 끝단에 5,000N의 굽힘 하중과 65N⋅m의 비틀림 하중을 부여하고 파손단면의 직경과 거리를 이론적으로 계산하면 등가 비틀림 응력(Equivalent Torsional Stress, Te)은 약 121.8MPa정도이며 등가 굽힘 응력(Equivalent Banding Stress, Me)는 약 125.7MPa 정도로 계산되었고 이는 파손된 SM45C 재질의 항복응력 424MPa에 비교하였을 때 약 3.37∼3.5의 안전율을 가지는 것으로 판단하였다. 또한 동적 하중계수를 각각 1.15를 선정하여 계산했을 경우에도 2.93∼3.04 정도의 안전율을 가지는 것으로 계산되었다.
3.2 SM45C의 피로응력 추정
기계구조용 탄소강의 경우 송풍기의 샤프트 또는 각종 기계의 회전축으로 주로 사용되는 재질로 사용되고 있으나 재질의 피로한도에 대한 S-N 선도를 구하기는 쉽지 않은 현실이다. 이는 제조공정에서 매 로트(Lot)마다 피로시험을 진행하여 평균화된 S-N 선도를 제공해주기에 시간과 비용 상의 이유로 인장강도 및 화학성분만을 성적서로 제공하고 있기 때문이다. 따라서 각 로트별 재료의 피로선도를 추정하기 위한 방안이 필요하게 된다.
일반적으로 사용되는 강재의 피로수명 사이클 곡선을 추정하는 방법은 다양하게 존재하나 기존의 일반적인 방법으로 최대인장강도(σultimate)를 기준으로 추정하는 방법이 있으며 이는 최대인장강도가 400MPa에서 1,400MPa 사이의 철강재에서 휨 하중이 작용하는 경우 1/4 사이클에서 최대인장강도를 적용하고 103 사이클에서 최대인장강도의 90%, 106 사이클에서 최대인장강도의 50% 강도를 추정하여 표현하는 방법이 있다.10,11) 그러나 이 방법에는 108 사이클 이상의 초고주기 피로수명을 추정할 수 있는 방안이 명시되어있지 않았다.
1010 사이클에서의 피로응력은 106 사이클 피로응력에 92%를 적용하여 추정한 결과 약 315MPa 정도의 값으로 추정하였다. 이와 관련해 추정된 각 사이클별 피로응력은 아래의 Table 5과 같이 정리하였다.
Fabian12) 등은 SAE 1045 강재의 피로곡선을 추정하는 공식을 발표하였으며 그 식은 아래와 같다.
| (4) |
여기에서, σa는 사이클에서의 피로응력, Nf는 사이클을 의미하며 각 알파벳에 해당되는 값은 아래의 Table 6과 같다.
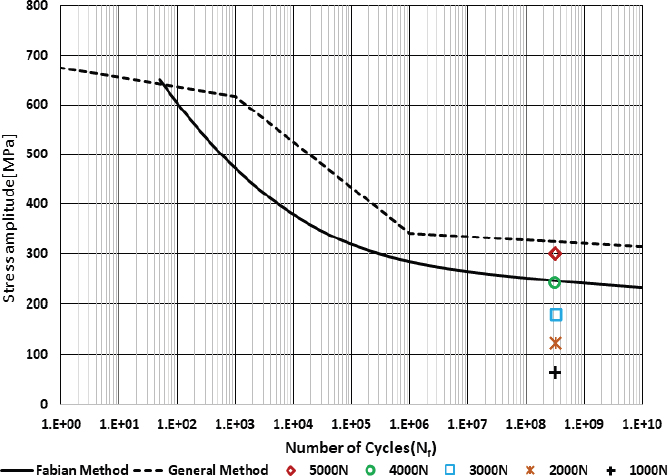
상기에 언급한 두 가지 방법에 의한 피로한도 곡선을 그려보면 다음 Fig. 6와 같이 편차가 발생되게 되게 되지만 이는 각 재료의 정확한 피로곡선을 구하는 시간적 또는 비용적 측면을 감안할 때 설계에 적용하기에 큰 무리가 없을 것으로 판단되며 보다 안전한 설계를 위해서는 Fabian의 수식을 적용하여 설계하는 것이 안전계수를 조금 더 가져갈 수 있는 방법으로 판단된다.
4. 구조해석
4.1 해석 설정 및 물성정보
해석을 위하여 Ansys Mechanical 2024 R1 Static Structure 모듈을 사용하여 해석을 진행하였다. 샤프트는 SM45C 재질로 설정하였고, 롤러베어링 틸팅 모사를 위해 베어링강 재질을 추가하였으며 적용된 재질속성은 아래 Table 7과 같다.
베어링의 자동조심 허용 각도를 구현하기 위하여 자동조심 롤러 베어링의 주 단면 형상을 모사하고 각각 외륜의 접촉면과 롤러 사이(A, B)의 비분리조건(No Separation)과 본드(Bond) 조건을 접촉조건으로 설정하여 해석을 진행하였다. 또한 파손된 단면의 형상변화에 따른 응력변화를 확인하기 위하여 0.5R과 2.5R의 라운드를 성형하여 해석을 진행하였다. 또한 샤프트 자체중량의 연관성을 확인하기 위하여 중력가속도 조건을 포함하였다. 세부 조건 및 입력 값은 다음의 Fig. 7과 Table 8과 같이 설정하였다.
4.2 유한요소 분할구성
유한요소해석(Finite element analysis, FEA)은 컴퓨터의 발달로 수치적 접근을 통하여 재료의 구조적 응력과 변형량을 확인해볼 수 있는 컴퓨터 시뮬레이션으로 근래에 들어 자주 사용되고 있다. 유한요소해석에서의 강성행렬은 아래의 식 5와 같다.
| (5) |
여기에서 K는 구조 강성행렬이고 Q는 구하고자 하는 미지수 또는 변위벡터를 의미하며, F는 하중 벡터를 의미한다.
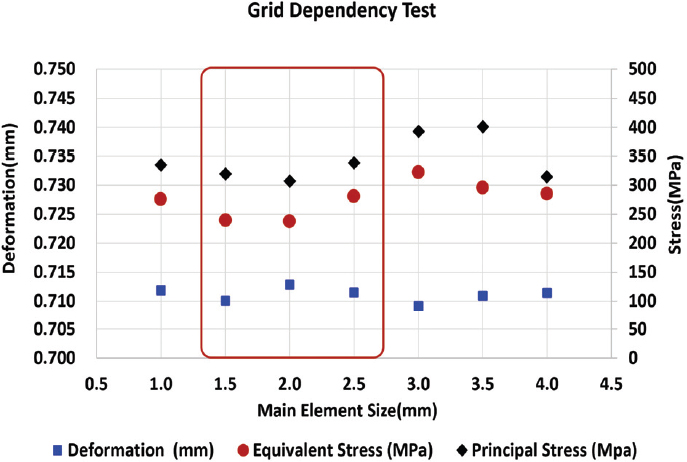
이번 연구에서는 파손된 단면에서의 응력거동을 확인하고 응력의 수준이 피로한도를 초과하는지에 대한 문제를 확인하고자 하였고 이에 따라 파손된 단면부근 및 최초 균열 발생 의심 지점에 격자를 집중하여 분포시켰으며 메인 요소의 크기를 변경해가며 격자의 품질을 확인한 결과 1.5∼2.5mm 사이에서 종횡비(Aspect Ratio), 왜곡률(Skewness), 야코비안 비(Jacobian Ratio)가 다른 요소 사이즈에 비하여 우수했다. 격자 의존성 테스트(Grid Dependence Test)결과는 아래의 Fig. 8과 같다.
상기 격자의존성 테스트 결과를 토대로 전체모델의 격자 크기는 2mm 이하로 설정하였으며 파손단면의 곡면부 격자 크기는 0.2mm를 적용하였고 구형 인플레이션(Sphere inflation) 2개를 6mm 크기로 록크와셔 키 측면부에 설정한 후 격자 크기는 0.1mm로 설정하여 진행하였다.
상기와 같이 설정된 조건에서 0.5R 샤프트 모델의 격자는 2,848,588개의 노드와 1,762,024개의 요소로 구성되었으며 각 격자는 2차 요소(Quadratic Element)로 구성하였다. 이때 사용된 격자의 종류는 Tet 10 요소가 1,749,234개, Hex 20 요소가 12,790개로 구성되었다. 같은 조건에서 축 단부 라운드 2.5R의 모델은 0.5R 모델보다 적은 2,766,145개의 노드와 1,759,978개의 요소로 구성되어 있었다. 각 모델별 메쉬 정보는 위의 Table 9와 같다.
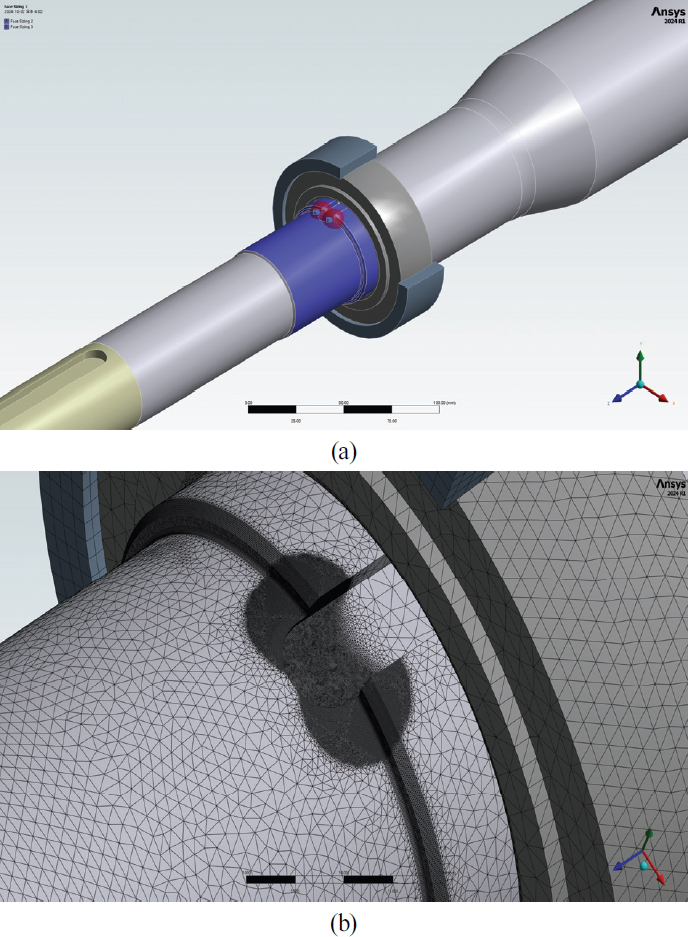
다음의 Fig. 9은 0.5R 샤프트 파손부위의 격자 구성 설정과 설정 후 구성된 격자의 분포 형상을 보여주고 있다. 또한 아래의 Fig. 10는 2.5R 라운드 샤프트의 베어링 축단부에서의 격자 분포를 보여주는 그림이다. 0.5R 샤프트는 0.5R 라운드 이후 로트너트용 나사가공을 위한 1mm의 모떼기를 진행한 상황이고 2.5R 샤프트는 별도의 모떼기 없이 나사를 가공하는 것으로 구성된 모델이다. 기존의 파손된 샤프트를 교체하기 위하여 직경 및 길이를 변화시킬 수 없는 상황에서 단차부의 가공 라운드만을 변화시켜 응력집중을 저감하기 위한 방안으로 고려되었다.
5. 해석결과
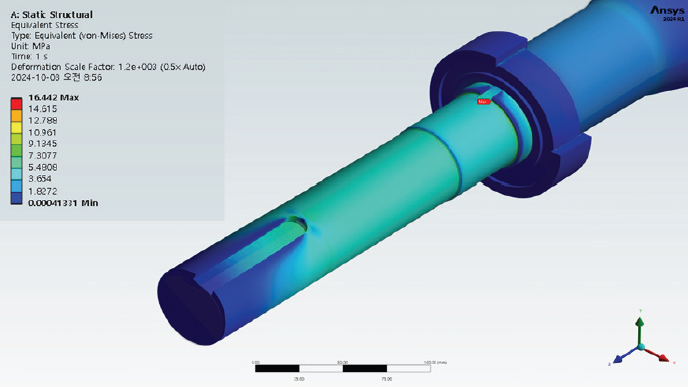
11kW의 동력을 전달하기 위한 순수 비틀림에 의한 응력은 약 16.442MPa로 해석되었으며 이는 피로파손을 일으키는 주요 원인은 아닌 것으로 판단된다. 또한 이론적 계산에 의한 순수 비틀림 응력의 6.23배 정도로 계산되었으나 이는 축의 단면적 변화에 따른 노치효과(Notch effect)에 의한 응력집중 및 로크와셔용 고정키(Key-way) 절삭의 효과로 판단된다. 비틀림 응력에 의한 해석 결과는 Fig. 11과 같다.
아래의 Fig. 12의 (a)와 (b)는 자동조심 베어링에 의한 조심 각이 허용되는 0.5R 샤프트와 2.5R 샤프트에 벨트텐션 5,000N, 비틀림 토크 65N⋅m의 하중을 가할 때의 해석결과이다. (a)의 경우 풀리 조립 끝단부의 최대 처짐은 약 0.746mm 정도가 발생되고 이때 최대 등가응력은 약 300.22MPa 정도로 파손부위에서 발생된 것을 확인하였다. 이는 약 3.21 ×108 회전 정도의 사이클에서 피로파손이 유발될 수 있을만한 응력으로 판단된다.
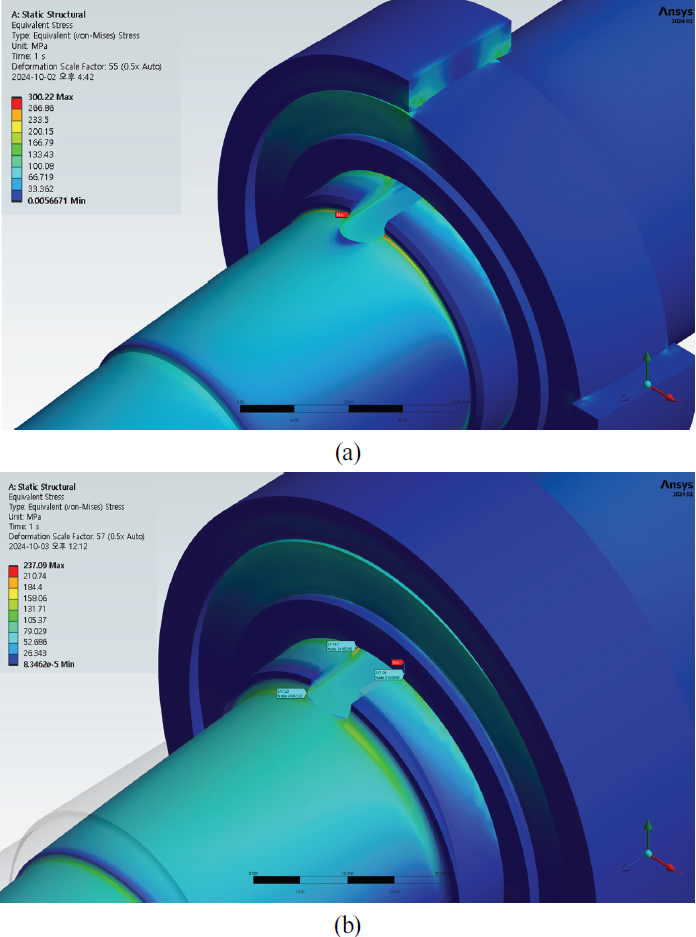
Equivalent Stress Distribution under No Separated Condition at Belt Tension 5000N, Torque 65N⋅m (a) 0.5R Shaft, (b) 2.5R Shaft
그러나 (b)의 2.5R 샤프트에서는 최대 등가응력 발생부위는 베어링 접촉면으로 이동하였으며 최대 등가응력도 237.09MPa 정도로 약 21% 정도 감소하였다.
아래의 Fig. 13은 베어링에서 자동조심이 가능한 경우와 가능하지 않은 경우에서의 전체적인 변형량을 비교한 그림이다. 자동조심이 허용되는 경우 임펠러의 중량 하중이 가해짐에도 샤프트의 중앙부위가 상부방향으로 변형되어 올라오는 것을 확인할 수 있었으며 (a)에서의 최대 변형량은 약0.482mm이었으며 (b)에서의 최대 변형량은 약 0.746mm로 약 54.8% 정도의 변형량이 증가하였고 베어링 사이에서의 중심부 최대 변형량은 Y 방향으로 +0.235mm 정도였다.

0.5R Shaft Deformation at Belt Tension 5000N, Torque 65N⋅m (a) Bonded Condition, (b) no-separated condition
일반적으로 자동 조심형 롤러 베어링과 깊은 홈 볼 베어링의 허용 조심 각은 베어링의 크기와 정밀도, 제조사마다 다르게 설정된다. Table 10는 NSK사 베어링별 허용 조심 각 자료이다.9)
아래의 Fig. 14은 베어링에서 자동조심이 불가능한 경우에서의 등가응력 분포도를 나타내고 있다. 0.5R 반경의 경우자동조심이 가능할 때보다 최대등가응력의 약 14MPa 정도 증가하는 양상을 보이고 있으며 최대 응력 점은 같은 위치에서 나타났다. 그러나 2.5R의 경우 Fig. 12(b)와 달리 최대 응력 점의 위치가 달라지는 것으로 나타났다.
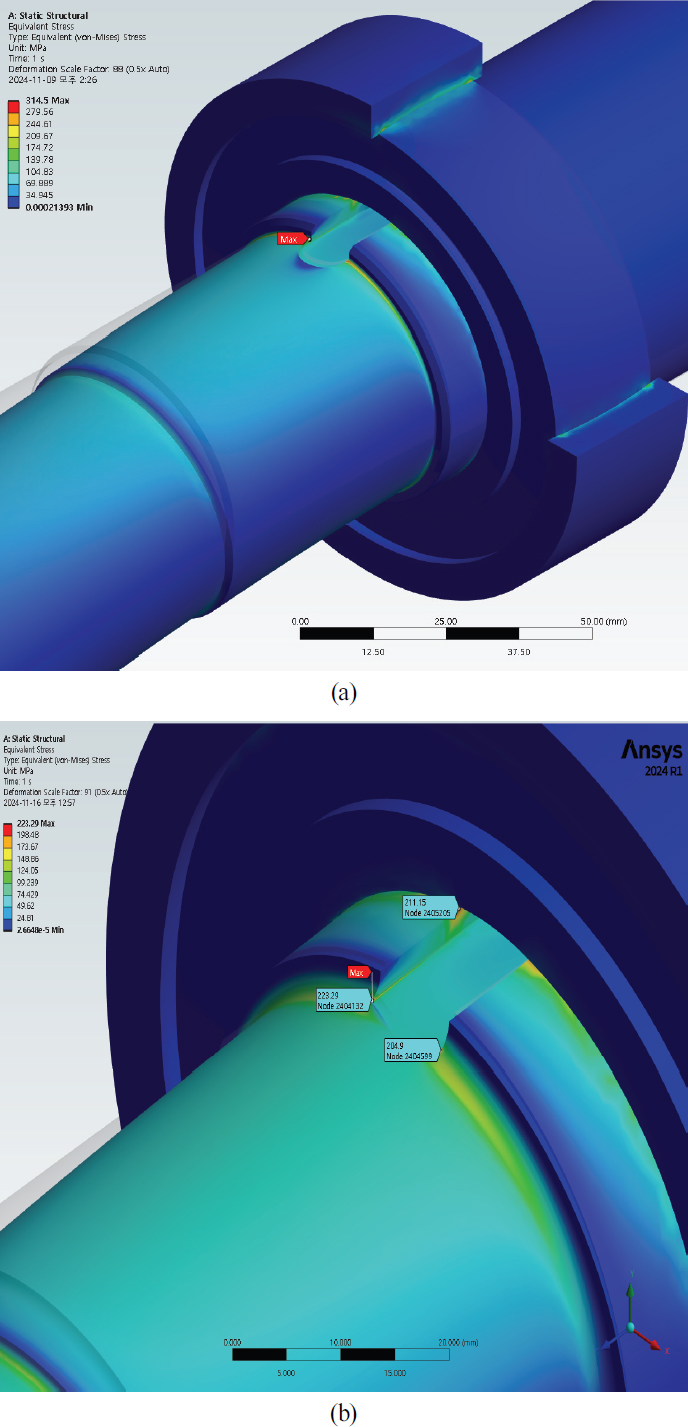
Equivalent Stress Distribution under Bond Condition at Belt Tension 5000N, Torque 65N⋅m (a) 0.5R Shaft, (b) 2.5R Shaft
베어링의 자동조심 작용에 의해 틸팅이 허용되는 조건을 롤러(Roller) 조건으로 설정하고 깊은 홈 볼 베어링처럼 자동조심 허용 각도가 매우 적은 경우를 볼(Ball)의 조건으로 설정하여 비틀림 토오크를 65N⋅m로 고정한 후 각 벨트 텐션하중을 1,000N∼5,000N까지 부가하여 해석한 결과를 정리하면 다음의 Table 11과 같다.
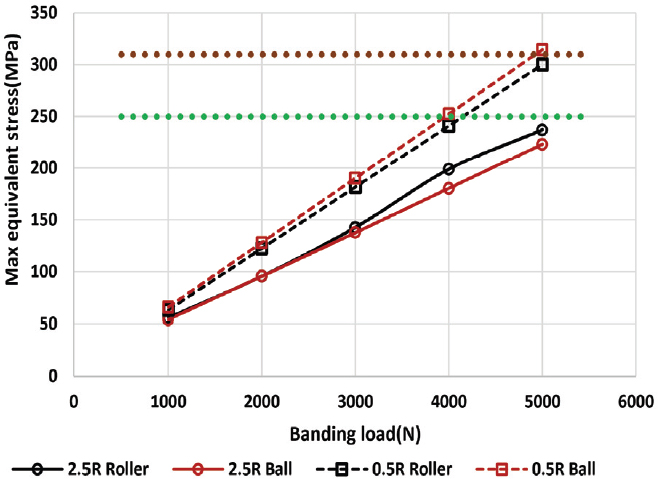
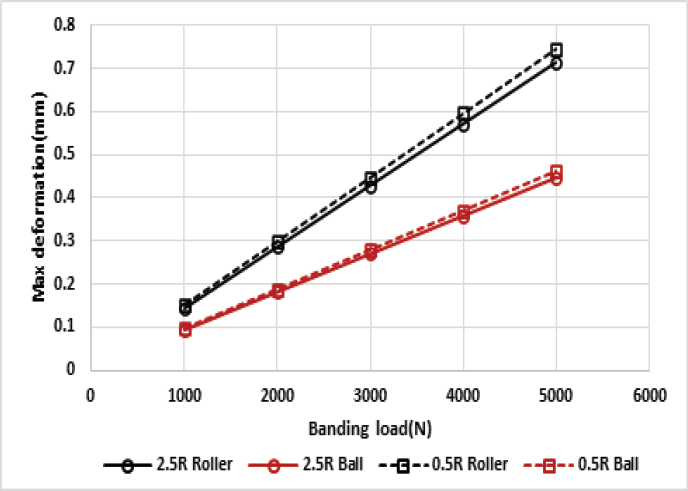
각각의 결과 값을 응력과 처짐량을 기준으로 그래프로 그려보면 다음의 Fig. 15과 Fig. 16처럼 나타나게 된다.
Fig. 15에서 초록점선(Green Dotted Line)과 갈색점선(Brown Dotted Line)은 Fabian 방식과 최대인장강도(σultimate)를 기준에 의한 1010사이클 피로수명 응력을 표시하였다. 베어링의 로크너트 축단부의 반지름을 2.5R로 가공 제작하는 경우가 0.5R로 제작 후 1mm 모떼기를 하는 경우보다 응력이 현저하게 나타나게 되며 이는 약 5000N의 인장력이 발생하더라도 약 250MPa 이하의 응력으로 1010사이클 이상까지 안전하게 구동될 수 있을 것으로 판단된다. 0.5R로 가공하는 경우에는 4,000N∼5,000N 사이에서 Fabian 방식에서는 파괴가 일어날 수 있으나 최대인장강도 4점식에서는 아직 안전한 것으로 평가된다. 0.5R의 롤러베어링의 곡선 중 4,000N 결과는 최대응력 발생 지점이 축 단차부에서 베어링 접촉부위로 이동하며 발생된 응력의 증가로 판단된다.
다음의 Fig. 16은 최대 변형량 그래프로 0.5R 샤프트의 최대 등가응력에서 곡선형으로 발생하는 것과는 별개로 일정한 응력대비 변형량을 보이고 있다. 이는 엘리먼트가 집중된 부분보다 멀리 떨어진 일정크기의 메쉬로 인하여 격자의 영향을 덜 받는 것으로 판단된다. 그러나 축단차부의 반경지름의 크기 변화에 따른 변화량은 명확히 구분될 정도의 결과를 보이고 있으며 축 단부 반경이 작은 경우 조금 더 큰 변형량을 보이는 것으로 나타났다.
5.1 벨트의 적정 인장력 검토
상기 파손된 공조기용 송풍기의 모터동력은 11kW이고 송풍기의 풀리 피치 지름은 165mm 회전수는 1621rpm이었다.
| (6) |
64.8Nm의 토크를 전달하기 위하여 슬립이 없다고 가정하면
| (7) |
약 785N의 힘이 필요하게 된다.
벨트구동용 송풍기에 풀리 및 고무벨트를 설치하는 경우 축에 작용하는 굽힘 응력을 정확히 추정하기에는 어려움이 있으나 KS규격 또는 벨트회사의 카탈로그 등을 통하여 추정이 가능하다. KS규격13)에 따른 B형 고무벨트의 경우 초기 장력은 약 400N 정도이고 벨트 제조사 매뉴얼14∼17)에 따르면 11kW 동력전달의 경우 B형 4가닥 초기장력은 1가닥 당 250∼300N 정도로 권고되고 있다. 따라서 적정수준의 전체 장력은 최소 1,000N에서 최대 1,600N 정도의 인장력이 적절한 것으로 판단된다. 상기 해석결과에서 파손된 샤프트는 4,000N까지는 피로한계 이내인 것으로 판단되며 파손 시 약 4,000N∼5,000N 이상의 벨트 인장력이 가해진 것으로 추정된다. 이는 B형 벨트 1본 당 파단강도가 약 6,800N18) 이상인 것을 감안하면 샤프트가 피로파손을 일으키는 굽힘 응력의 1.36∼1.7배 정도의 강도로 벨트 1가닥만으로도 샤프트를 피로파손에 이르게 할 수 있다.
5.2 파손단면의 형상 및 비교
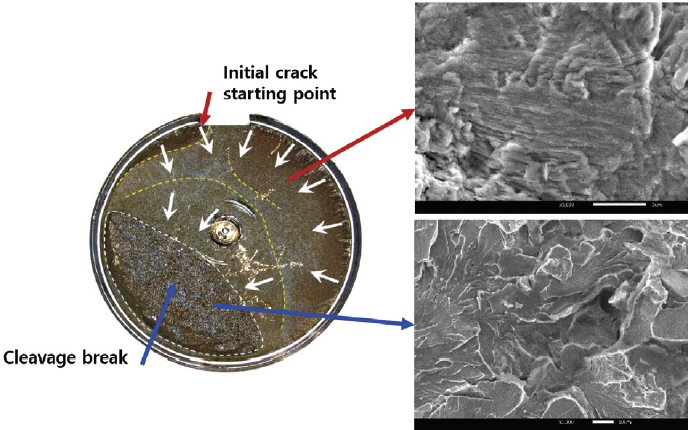
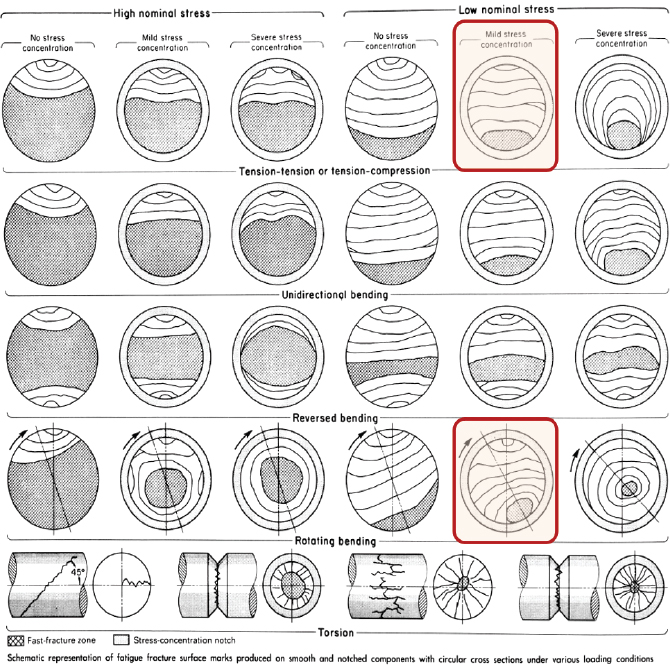
아래 Fig. 17은 한국재료연구원의 파손단면에 대한 분석 보고서의 내용을 인용하였으며 Fig. 18는 ASM Handbook19)상의 그림으로 각 부하의 크기 및 종류와 부하방향에 따른 파손 형태의 그림이다. 비틀림과 굽힘 동시에 받는 샤프트의 저 부하 피로의 형상과 매우 비슷한 형상을 띄고 있다.
한국재료연구원에 의뢰한 시료의 파손 단면에서의 미세 조직 사진과 파단형상의 분석결과에 의하면 최초의 균열(Crack) 시작점은 로트너트 고정용 키 가공부에서 시작된 것으로 판단했으며 구조해석의 결과에서도 같은 위치에서 최대 응력이 발생하는 것으로 나타났다. 따라서 상기의 결과들을 종합하여 판단해보면 벨트 장력에 의한 회전축의 굽힘 하중이 적정장력 이상으로 부가되어 초고주기 피로 파손(Very High Cycle Fatigue)으로 판단하는 것이 타당할 것으로 판단된다.
6. 결 론
본 연구의 결과를 요약하면 다음과 같다.
- 1) 벨트에 의한 과도한 인장력은 초고주기 피로현상에 의해 108 사이클 이상에서도 파괴를 일으킬 수 있으며 일반적인 106 사이클에서의 응력하중보다 낮게 설계하여야 한다.
- 2) 노치부의 라운드 크기를 0.5R에서 2.5R로 크게 하는 것만으로도 최대 등가응력을 10∼20% 이상 감소시킬 수 있는 것으로 나타났다.
- 3) 자동조심 롤러 베어링과 깊은 홈 볼 베어링의 각도 틸팅 효과에 의해 자동조심형의 변형량이 더 크지만 응력의 위치분산 효과가 커지고 최대 등가응력 발생 위치에서의 최댓값은 더 작게 작용된다.
- 4) 파손된 샤프트는 4,000∼5,000 N 정도의 과도한 인장력으로 샤프트를 당기며 구동되어 이로 인한 피로가 축적됨에 따라 고주기 피로파손을 일으킨 것으로 추정된다.
- 5) 현재 2.5R 상태로 수정 보완된 샤프트는 22년 12월말 교체이후 벨트의 스팬 길이 중앙에서 약 4kg의 누르는 힘으로 벨트 처짐량 10mm 정도로 수정 보완하였으며 이는 초기 장력 약 400∼500N 정도로 추정되고 축에 1,600∼1,800N의 굽힘 하중을 발생시킬 것으로 예상되며, 현재 약 1.284×109사이클 이상 정상작동 하고 있는 것으로 파악되었다.
References
-
Tae An Kim, Hyung Joon Park, and Seung Ho Han, 2018, “Shape Optimization Design of an Automotive Drive Shaft for Improving Fatigue Life” Transactions of the Korean Society of Mechanical Engineers - A, vol. 43, no. 1, pp67-72.
[https://doi.org/10.3795/KSME-A.2019.43.1.067]

- Chung-Seog Oh, 2015, “The Advent of the Era of Ultra-High-Cycle Fatigue” Journal of the KSME, 55(2), 45-49.
-
Won-Jon Yang and Chung-Seog Oh, 2022 “Application of Fractography and Finite Element Analysis Adopting Elastic Foundation Stiffness to Improve Fatigue Life of Main Shaft in Mechanical Press.” Journal of the Korean Society for Precision Engineering, vol. 39, no. 5, 2022, pp363-369.
[https://doi.org/10.7736/JKSPE.022.011]

-
C.M. Suh, C.H. Suh and M.S. Suh, 2013, C.M. Suh et al.. “VHCF Characteristics of SCMH2 Steel Depending on the Surface Treatment Conditions.” Journal of Welding and Joining, vol. 31, no. 4, pp47-53.
[https://doi.org/10.5781/KWJS.2013.31.4.47]

-
Byeong Kyou Jin, Ki Beom Park, and JangBom Chai, 2014, “Fatigue Life Evaluation of Turbine Shaft Using Applied Shaft Stress.” Transactions of the Korean Society of Mechanical Engineers - A, vol. 38, no. 4, pp437-442.
[https://doi.org/10.3795/KSME-A.2014.38.4.437]

- Jun-Young Kim, Yeong Jun Yu, and Chul-Hee Lee, 2023. “Accelerated Life Test Selection Study for Life Evaluation of Engine Type Drive Axle for Forklift.” Journal of Drive and Control, 20(3), 9-14.
- KS D 3752:2019 : “Carbon Steel for Machine Structural Use”
- Yang Won-Jon, Park I-Ho, Ha Young-Soo, Oh Chung-Seok, 2022, “Technical Support Report on Analysis of Causes of Shaft Damage for Centrifugal Fans”
- NSK Rolling Bearing Catalogue CAT. No. 1102f 2016K, pp B178-B201.
-
Chaminda S. Bandara, Sudath C. Siriwardane, Udaya I. Dissanayake, Ranjith Dissanayake, 2015, “Developing a full range S–N curve and estimating cumulative fatigue damage of steel elements” Computational Materials Science 96(2015) Page 96∼101), ELSEVIER
[https://doi.org/10.1016/j.commatsci.2014.09.009]

-
Kim, Kwang Jin, Kim, Dae Yong 2018, “Development of the Algorithm and Software for Optimized S-N Fatigue Test of Structural Steels” Journal of Korean Society of Steel Construction Vol.30, No.3, pp.137-144, June, 2018
[https://doi.org/10.7781/kjoss.2018.30.3.137]

-
Fabian Weber, Janina Koziol, and Peter Starke, 2023, “Stress Life: A Short-Time Approach for the Determination of a Trend SN Curve in and beyond the HCF Regime for the Steels 20MnMoNi5-5 and SAE 1045”, Materials 16.11 (2023): 3914.
[https://doi.org/10.3390/ma16113914]

- KS M 6535:2018 : Classical V-Belts for Power Transmission
- Dongil Belt “Power Belt Design Manual” PT-M-190401-KR
- SKF Power Transmission Belt Catalogue, 2016, PUB PT/P1 06875/3EN, pp 69-71
- Mitsuboshi Design Manual V-Belt RMA Catalogue, 2014, V8300501504sg03685906, pp 3.3-3.8
- Gates Industrial V-Belt Drive Design Manual, 2004, E2/20070ED2004, pp30-34
- V-Belt Test Report JNHUNG-QAW231120 Wrapped B Type
- ASM International Materials Information Society ASM Handbook Volume 12: Fractography, Fig. 48 Schematic representation of fatigue fracture surface marks