대체모델 기반 산업용 공기 원심압축기 공력효율 최적화에 관한 수치적 연구

1. 서 론

터보형 압축기의 한 종류인 원심압축기는 축류 압축기에 비해 효율과 단당 압축비가 높고, 같은 회전수에서 넓은 운용범위(turndown ratio)를 확보할 수 있는 장점이 있다. 또한, 상대적으로 구조가 간단하고 소형으로 제작할 수 있는 장점을 바탕으로 석유 및 가스산업, 제조산업 압축공기 공급 등 다양한 용도로 사용되고 있다.

산업 및 서비스업에서 사용되는 많은 공기압축기는 운전조건이 크게 변하지 않는 조건에서 장시간 작동된다. 이에 따라 산업 및 서비스업 소비 전력 중 약 20%를 차지하며 연간 약 4조원의 전기료가 발생 된다⁽¹⁾. 따라서 에너지절약 및 비용 절감을 위해서 산업용 공기 원심압축기의 효율을 증가시키는 노력이 계속되고 있다.

일반적인 원심압축기는 임펠러(impeller), 디퓨져(diffuser) 및 볼루트(volute)로 구성된다. 이중 임펠러 및 디퓨져는 원심압축기 효율에 있어 매우 중요한 부분으로 압축기 설계의 핵심이 되는 부분이다. 임펠러 및 디퓨져의 3차원 형상 설계 시 많은 설계변수를 설정해야 하며, 이러한 설계변수들은 서로 비선형적인 관계로 원심압축기의 효율에 영향을 미친다⁽²⁾. 이러한 이유로 원심압축기 최적화를 이용한 설계개선은 도출된 형상에 대한 많은 수의 유동해석이 필요하므로 최적 설계 결과 도출까지 많은 계산 비용(computational cost)이 소모된다. 따라서 최적화 기법을 이용한 효율적인 설계개선 방법이 필요하다.

원심압축기 최적화 중 가장 많은 시간을 차지하는 부분은 유동해석이다. 따라서 원심압축기 최적화를 위해서 실제 유동해석 대신 해석모델에 대한 대체모델을 이용하는 대체모델(surrogate model) 최적 설계가 많이 이용된다. 대표적인 대체모델로는 방사기저함수망(RBFN: radial basis function network), 반응면기법(RSM: response surface method), 크리깅(kriging) 등이 있다⁽³⁾.

Bonaiuti 등⁽⁴⁾은 천음속 원심압축기 효율과 압력비를 향상시키기 위해 임펠러 형상에 대한 최적 설계를 실험계획법을 사용하여 수행하였다. 반응면기법 대체모델을 활용하여 Seo 등⁽⁵⁾은 공기 원심압축기 임펠러의 자오면 및 블레이드 각도 θ를 대상으로 최적화를 수행하였다. Ma 등⁽⁶⁾은 원심압축기 임펠러 블레이드 각도 β와 자오면 형상을 설계변수로 하여 방사기저함수망 기법을 사용하여 최적화를 수행하였다. Kim 등⁽⁷⁾은 방사기저함수망 모델을 사용하여 원심압축기의 압력비를 향상시키기 위한 연구를 수행하였다. 크리깅 기법을 사용하여 Whang 등⁽⁸⁾은 원십압축기 임펠러 블레이드 각도 β를 설계 변수로 하여 최적화를 하였다. 이처럼 기존 원심압축기 최적화 연구는 임펠러의 최적화에 제한된 경우가 대부분이다.

본 연구에서는 실제 산업에서 사용되고 있는 공기 원심압축기를 개보수하는 과정에 최적화 기법을 도입하여 임펠러와 디퓨저를 동시에 최적화하였다. 따라서 기존 압축기 케이싱과 볼류트는 그대로 사용한다는 제한조건을 두고 최적 설계를 수행하였다. 이에 따라 임펠러 허브 자오면 형상 및 블레이드 각도 β 분포, 디퓨져 블레이드 각도 β 분포에 대해서 최적화 설계를 수행하였다. 최적화 수행에 있어서 방사기저함수망을 활용한 대체모델 기법을 이용하며 도출된 형상에 대한 성능 해석 및 유동특성 분석을 하였다.

2. 최적화기법

2.1 최적화 절차

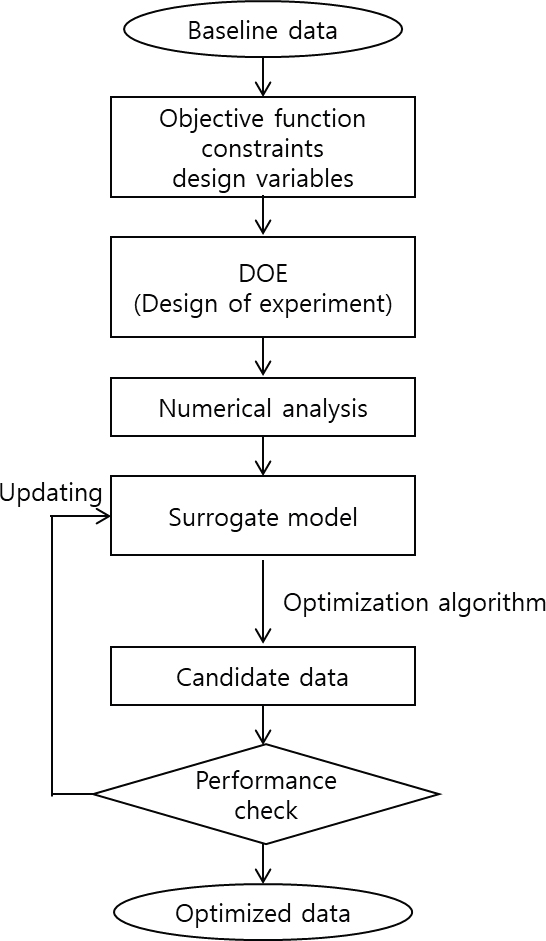
본 연구에서는 Numeca사의 FINE/Design 3D 플랫폼을 이용하여 최적화를 진행하였다. FINE/Design 3D 플랫폼은 터보기계 설계프로그램인 Concept NREC사의 AxCent와 연동하여 실험계획법(DoE: design of experiment) 및 대체모델(surrogate model)을 기반으로 최적화를 수행하였다. Fig. 1은 본 연구에서 사용한 대체 모델기반 최적화(SBO: surrogate–based optimization) 기반 원심압축기 형상 최적화 순서도이다. 기준데이터(baseline data)는 최적화 대상의 기존 데이터이며 최적화 절차를 통해 도출된 최적화 데이터와의 비교군으로 활용된다. 다음으로 목적함수, 설계변수 및 제한변수를 정의한다. 목적함수(objective function)는 최대화 혹은 최소화하고자 하는 대상이 되는 함수를 의미한다. 제한변수(constraint)는 최적화 절차에서 주어진 제약조건을 의미하며 특정 값의 범위 내에 있어야 한다. 설계변수(design variables)는 최적화 문제에서 최적값을 찾기 위해 조정할 수 있는 변수이다. 이 변수들은 최적화 알고리즘이 탐색하는 변수들로, 목적함수의 값에 영향을 주며 최적값을 결정한다. 변수 설정값들을 기반으로 실험계획법을 수행하였다. 실험계획법은 통계적 기법을 활용하여 데이터베이스를 설계하고 분석하는 방법론이며 최소한의 데이터 생성을 통해 최대의 정보를 얻는 것이 목표이다. 실험계획법을 통해 도출한 데이터를 기반으로 유동해석을 통해 대체모델을 생성한다. 대체모델은 계산 비용이 많이 드는 유동해석을 대신하여 사용할 수 있는 수학적 모델이다. 대체모델은 입력값과 출력값 사이의 관계를 근사화하는 방식으로 결과를 빠르게 도출한다. 이러한 대체모델을 기반으로 최적화 알고리즘(optimization algorithm)을 사용하여 후보 데이터(candidate data)를 도출하고 유동해석을 통한 성능검증(performance check)을 통해 기준데이터와 값을 비교하였다. 만약 성능검증 결과 기준데이터와 비교하여 개선 폭이 크지 않다면 해석결과를 대체모델에 추가시키는 방식으로 대체모델의 정확도를 높인다.

Fig. 1

Flow chart of surrogate model optimization

2.2 기준데이터

2.2.1 최적화 대상 압축기

본 연구에서는 총 3단으로 구성된 일체형 기어 원심압축기의 마지막 단을 대상으로 형상 최적화를 수행하였다. 대상 원심압축기는 해외업체에서 제작된 산업용 공기 압축기로 작동 유체는 대기 중 공기이며 전체 출력은 1,500 hp, 토출압력은 150 psi(g)이다. 대상 원심압축기는 임펠러, 베인디퓨져 그리고 볼류트로 구성되어 있으며 본 연구에서는 볼류트의 형상은 최적화 대상에서 제외하였다. 3차원 형상 도출을 위하여 대상 압축기의 임펠러, 베인디퓨져를 광학 형상 스캐닝을 통하여 Fig. 2와 같이 형상 데이터를 확보하였다.

Fig. 2

Optically scanned centrifugal compressor impeller (left) and vaned diffuser(right)

2.2.2 목적함수, 제한변수 및 설계변수

원심압축기 형상 최적화를 위해 먼저 목적함수를 설정하였다. 대상 압축기는 정격운전 조건에서 장시간 운전되는 산업용 공기 압축기로 소요 동력(power) 감소를 위해 고정된 운용조건(회전수, 압력비, 유량)에서 최대의 효율을 내는 방향으로 최적화를 진행하였다. 따라서 아래의 등엔트로피 효율(isentropic total-to-total efficiency)을 목적함수로 설정하였다.

$\[ {\eta }_{TT}=\frac{{\left(P_{05}/P_{01}\right)}^{\left(\gamma -1\right)/\gamma }-1}{T_{05}/T_{01}} \]$

(1)

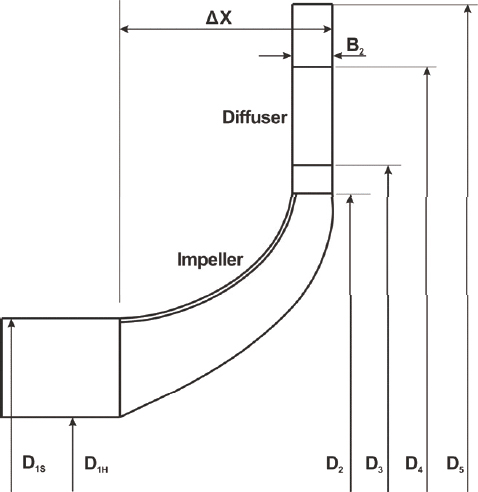
본 최적화 연구는 최적화된 임펠러 및 베인디퓨져를 실제 산업용 원심압축기에 장착하여 압축기의 효율 향상 및 소요동력 감소를 목표로 한다. 따라서 기존 원심압축기 형상을 크게 변경시키지 않는 방향으로 제한변수 설정을 진행하였다. Fig. 3은 대상 압축기의 임펠러 및 디퓨져 자오면 형상(meridional plane)이다. 원심압축기의 전체적인 형상은 허브와 쉬라우드의 자오면 형상 및 날개 각도 β 분포 때문에 결정된다. 압축기의 입출구 위치 및 형상은 각각 2단 출구 및 3단 볼루트 입구에 의해 결정되므로 제한변수로 설정하였다. 블레이드 각의 경우 입구 유동 각이 고정되어 있으므로 임펠러 블레이드 입구 각도는 제한변수로 설정하였으며 팁 간극 또한 제한변수로 설정하였다. 3단 원심압축기의 임펠러 케이싱이 일체형 기어 원심압축기의 케이싱에 고정되어 있어 임펠러의 슈라우드 형태 또한 고정변수로 설정하였다. Table 1은 제한변수로 설정한 변수들을 보여준다.

Fig. 3

Fixed parameters of the impeller and vaned diffuser

Table 1

Specification of fixed parameters

압축기 설계변수 설정 및 변경을 위해서 Concept NREC사의 터보기계 설계프로그램인 AxCent ver. 8.10.0 프로그램을 사용하였다. 설계변수 조정을 통한 원심압축기 형상 변경을 위해 베지어 곡선 제어점(bezier curve control point)을 이용하였다. 베지어 곡선을 이용하여 제어점 수를 최소화하는 동시에 임펠러 및 디퓨져를 다양한 형태로 변경할 수 있다.

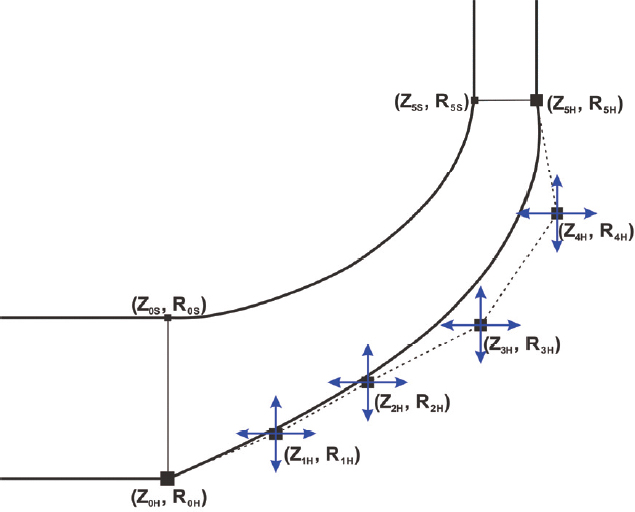
Fig. 4는 원심압축기 임펠러 허브의 자오면 형상 및 베지어 곡선 제어점을 보여준다. 압축기의 전체 크기를 고정했기 때문에 임펠러 입출구의 허브 및 쉬라우드 제어점(Z₀, R₀), (Z₅, R₅)의 좌표를 고정하였으며, 임펠러 입구 출구 사이의 제어점(Z_1∼4, R_1∼4)을 변경하여 자오면 형상을 변경시켰다. 추가 설계변수로써 임펠러 및 디퓨져의 날개 각을 설정하였다. Fig. 5 (a) 및 (b)는 각각 임펠러 및 디퓨저 허브와 슈라우드의 β 분포 제어점 및 변경 범위를 보여준다. 날개각 β 는 임펠러 및 디퓨져 날개의 전연(leading edge)에서 후연(trailing edge)까지의 베지어 곡선으로 표현하였다. 임펠러의 입구 날개각 β_i0 는 설계점유량과 회전 속도를 고려하여 설계된 값이므로 고정했으며, 임펠러 출구 날개각 β_i9 는 백스윕(back sweep) 각도로 설정되므로 변경하지 않았다. 따라서 임펠러 날개 각은 LE와 TE 사이의 베지어 곡선 제어점을 변경하여 최적화를 진행하였다. 이때 임펠러 출구의 경사각(lean angle)은 고정했다.

Fig. 4

Control points of the impeller hub meridional contours

Fig. 5

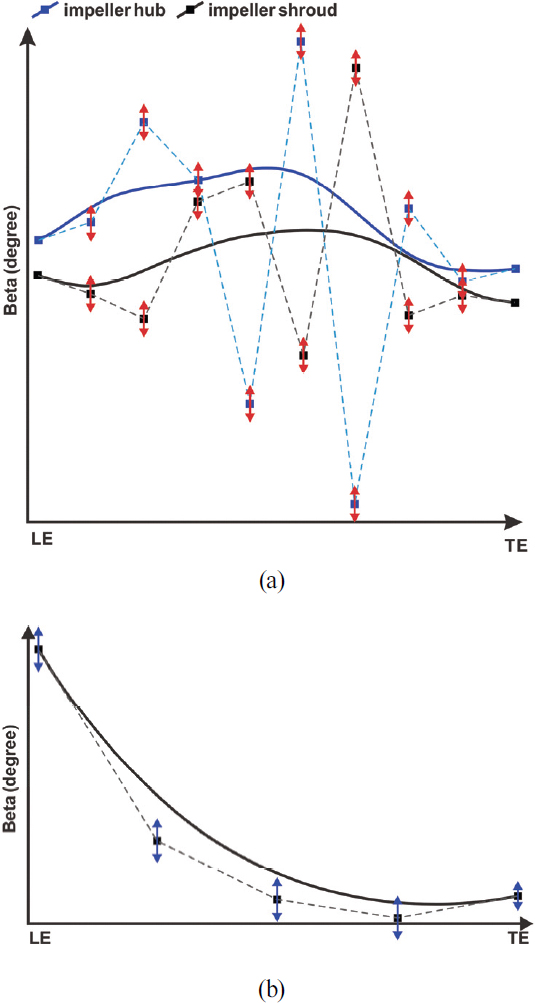
Control points of the β distributions and its range of variation for the (a) impeller and (b) diffuser

디퓨져 날개각 β_d의 경우(Fig. 5 (b)) 디퓨저는 2D 형상 블레이드이므로 허브와 슈라우드의 날개 각이 자오면을 따라 같다. 디퓨져 날개 각은 전연부터 후연까지의 베지어 곡선 제어점을 모두 변경시켰으며 후연의 베지어 곡선 제어점은 볼루트와의 매칭을 고려하여 그 외의 베지어 곡선 제어점보다 50% 수준으로 제한하여 변경시켰다. Table 2는 설계변수로 설정한 베지어 곡선 제어점의 범위를 나타낸다.

Table 2

Specification of design parameters

2.4 대체모델

대체모델 기반 최적화 연구에서 대체모델의 정확도는 최적화에 드는 시간 및 정확도에 큰 영향을 미친다. 본 연구에서는 LCVT DoE 결과에 Tuned 방사형 구조신경망(TunedRBFN: Turned radial basis function network) 알고리즘을 적용하여 대체모델을 형성하였다. TunedRBFN은 패턴 인식 및 함수 근사에 사용되는 방사기저함수망(RBFN: radial basis function network)의 한 종류이며 각 데이터 포인트의 값을 정확하게 예측하고 데이터 사이의 영역을 높은 정확도로 보간하는 함수를 생성하는 것을 목표로 한다. 기본적인 RBFN의 함수는 식 (2)와 같은 형태이다.

$\[ f\left(x\right)=\sum _{i=1}^p{w}_i\varphi \left(‖x-x_i^{data }‖\right) \]$

(2)

여기서 p 값은 은닉층(hidden layer)의 수이며 wi는 각 은닉층에 대한 가중치이다. $$ \varphi \left(‖x-x_i^{data }‖\right)$$는 방사기저함수이며 일반적으로 가우시안 함수로 표현된다⁽¹¹⁾. $$ ‖x-x_i^{data }‖$$는 기준값과 입력값 사이의 오차(유클리드거리)를 나타낸다. 방사기저함수망은 입력값과 여러 기준값 사이의 오차 값을 방사기저함수를 통해 비선형 변환하여 출력값을 생성한다. 은닉층은 입력값이 기준값에서 멀어질수록 은닉층의 활성화 수가 감소한다. 이러한 방식으로 방사기저망함수는 복잡한 비선형 관계를 모델링 하는데 특화되어있어 원심압축기 형상 설계변수에 대한 대체모델 생성에 적합하다.

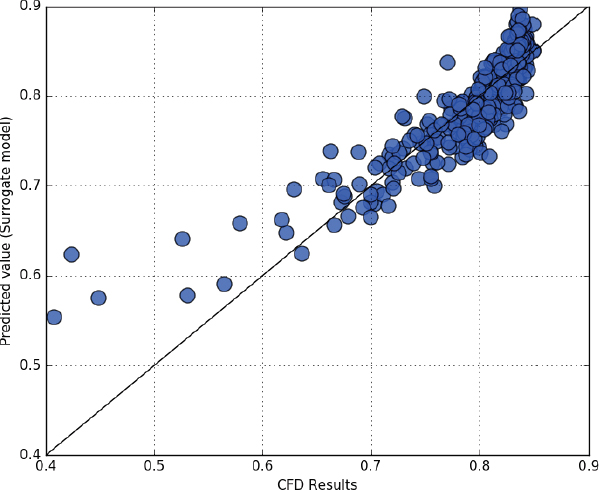
본 연구에서 생성한 대체모델의 정확성을 평가하기 위해 Leave-one-out 교차검증(LOOCV: leave-one-out cross-validation)을 수행하였다. Fig. 6는 310개의 DoE에 대한 유동해석 효율값(x축)과 개발된 대체모델로 예측한 효율값(y축)의 그래프이다. 유동해석을 통해 계산된 값과 대체모델이 예측한 값 간의 수정결정계수(R²_adj) 값을 기반으로 대체모델의 정확성을 평가한다. 즉 R²_adj > 0.9이면 대체모델의 정확도가 매우 높다고 판단하며 0.9 > R²_adj > 0.7이면 대체모델의 정확도를 최적화에 사용하기 적절하다고 판단한다. 본 연구에서 개발된 대체모델의 R²_adj 값은 0.883이며 충분히 높은 정확도를 갖고 있다.

Fig. 6

Results of the LOOCV(leave-one-out cross-validation) for the developed surrogate model

3. 최적화 결과

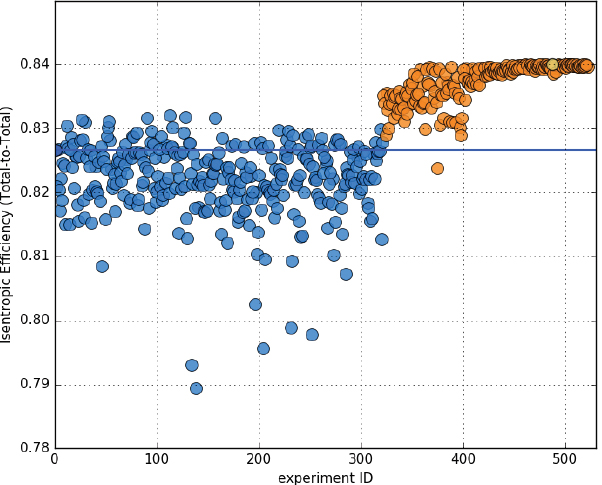
대체모델에 기반한 최적화 알고리즘을 통해 최적 형상후보를 반복적으로 생성하였다. 본 연구에서는 진화 알고리즘(EA: Evolutionary Algorithm)을 이용하여 최적화 형상을 도출하였다. 진화 알고리즘은 다양한 최적화 후보를 동시에 탐색 및 평가하여 최적값을 찾는 데 장점이 있다⁽¹²⁾. 또한, 국부 최적해(local optimum)에 수렴하지 않고 전역 최적화(global optimum) 가능성을 높여주어⁽¹³⁾ 형상 변화에 따라 비선형적으로 변하는 원심압축기 효율 최적화 문제에 적합하다. Fig. 7은 실험계획법 및 진화 알고리즘을 사용하여 도출한 압축기 형상을 유동해석 하여 계산한 효율 값이다. 그림에서 파란색 데이터는 실험계획법을 이용하여 도출한 압축기 효율 데이터이며 주황색 데이터는 대체모델에 기반한 진화알고리즘을 이용하여 도출한 압축기 등엔트로피 효율 데이터이다. 진화 알고리즘의 횟수가 늘어날수록 압축기의 등엔트로피 효율이 점차 증가하며 약 100회의 최적화 과정을 거침에 따라 효율이 약 84%로 수렴하는 것을 알 수 있다.

Fig. 7

Results of DoE(blue circle) and optimized compressor isentropic efficiency(orange circle)

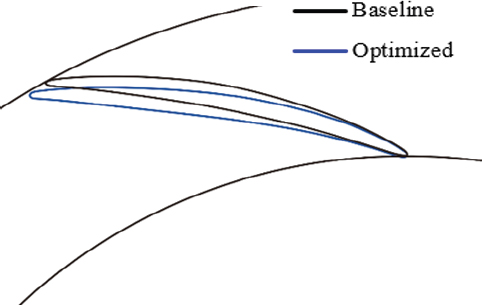
Fig. 8은 진화 알고리즘을 통해 도출한 압축기 중 가장 높은 효율을 보이는 형상에 대한 임펠러의 기존 형상과 비교한 그림이다. 최적화 형상에 대한 자오면의 경우 임펠러 입구 근처는 기존 형상에 비해 오목하게 설계되었으며 출구 근처에서는 볼록한 형상으로 설계되었다. 임펠러 블레이드의 경우 전연에서부터 코드길이 약 절반 위치까지는 블레이드 흡입면 쪽으로 볼록하게 설계되었으며 코드 길이 약 절반 위치부터 후연까지는 압력면 쪽으로 볼록하게 설계되었다. Fig. 9는 기존 베인디퓨져 형상과 최적화된 베인디퓨져 형상을 비교한 그림이다. 최적화된 베인디퓨져는 기존 베인디퓨져 형상과 비교하면 블레이드 사이의 유로가 좁혀지는 방향으로 설계되었다.

Fig. 8

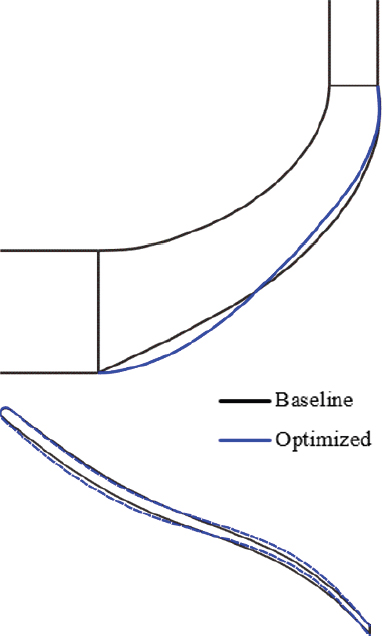
Geometries of the meridional contour(top) and blade profile bottom for the baseline and optimized impeller

Fig. 9

Geometries of the baseline and optimized vaned diffuser

4. 최적화 압축기 성능 분석

4.1 압축기 성능

최적화를 통해 도출된 형상에 대한 유동해석 결과분석을 통해 압축기 성능 비교를 하였다. 도출된 형상에 대하여 ANSYS사의 TurboGrid를 이용하여 정렬격자계를 형성하였다. 블레이드 표면 근처는 O형 격자계, 그 외의 영역에는 H/J/C/L형 격자계를 사용하였으며 블레이드와 허브, 슈라우드 벽면에서 y⁺가 3을 넘지 않도록 설정하였다. 도출된 임펠러 및 베인디퓨져의 총 격자수는 기존 형상 및 최적화 형상 모두 약 120만 개다. 유동해석은 3차원 난류 유동해석 상용프로그램인 ANSYS CFX를 사용하였으며 정상상태를 가정하여 수행하였다. 난류 모델은 k-w SST 모델을 이용하며 임펠러 출구 및 베인디퓨져 입구의 인터페이스는 mixing plane 모델을 이용하였다. 경계조건으로 압축기 입구에서 전압력(total pressure) 및 전온도(total temperature)를 고정하였고 베인디퓨져 출구에서 질량 유량을 고정하였다.

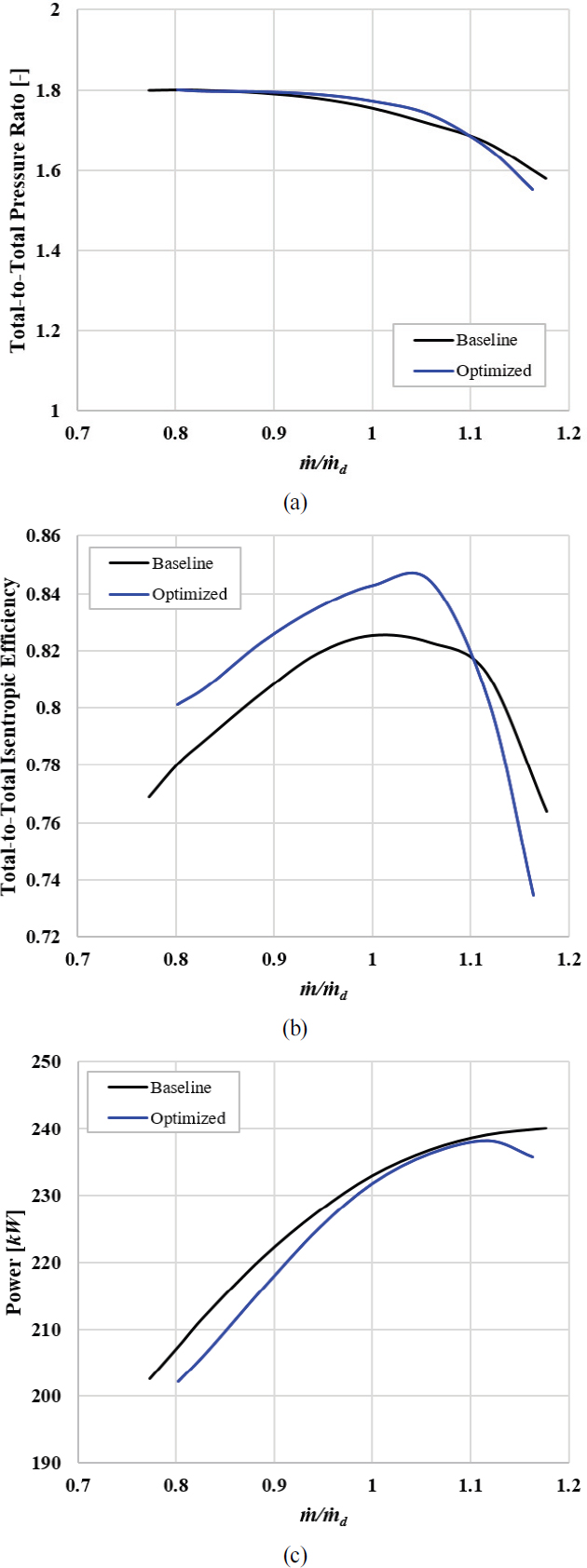
Fig. 10은 각각 유량 변화에 대한 기존 및 최적화 압축기의 (a)전압력비, (b)등엔트로피 효율 그리고 (c)소요 동력 계산 결과이다. 설계점에서 압축비는 기존 압축기 1.76에서 최적화 압축기 1.77로 유사하게 설계되었다. 설계 유량의 80∼110% 범위에서 최적화된 압축기는 기존 압축기 대비 1% 범위로 압력비가 높거나 유사한 값을 보인다. 등엔트로피 효율은 설계점에서 기존 압축기 82.5%에서 최적화 압축기 84.3%로 1.8% 증가하였으며 설계 유량의 80∼110% 범위 내에서 약 2%의 증가를 보인다. 이에 따라 압축기의 소요동력은 1∼4% 감소한 것으로 계산된다. 장시간 일정하게 운전되는 산업용 공기 압축기 특성을 고려한다면 최적화된 압축기의 등엔트로피 효율 향상으로 인한 소요동력 감소는 소요전력 및 운용비용 절감에 크게 이바지할 수 있을 것으로 판단된다. 설계 유량의 110% 이상에서는 최적화된 압축기는 기존 압축기보다 압력비와 등엔트로피 효율은 다소 감소하는 모습을 보인다. 다만 산업용 공기 압축기 특성상 모터 부하증가 이슈로 높은 유량에서 운전이 되지 않는 점을 고려한다면 압축비 문제는 없는 것으로 판단된다.

Fig. 10

(a) Total-to-total pressure radtio, (b) isentropic efficiency and (c) Power for both baseline and optimized compressor

4.2 압축기 유동특성 분석

기존 형상 및 최적화를 통해 도출된 형상에 대한 유동장 분석을 통해 등엔트로피 효율 및 소요동력 변화 원인을 분석하였다. Fig. 11은 기존 형상과 최적화 형상에 대한 설계점($$ \dot{m}/{\dot{m}}_d$$=1) 유량에서 50% 스팬의 마하수 분포를 나타낸다. 최적화 형상 압축기 임펠러 마하수 분포는 특히 흡입면(SS: suction side)측 후연 부근의 저유속 영역에서 크게 개선된 모습을 보인다. 최적화 임펠러 출구 근처에서 낮은 유속을 보이는 영역이 기존 형상에 비해서 작아졌으며 이는 낮은 에너지 영역이 작아졌음을 의미한다. 다른 스팬에서의 유동장에서도 매우 유사한 속도분포가 나타났다. 임펠러 출구에서 원주방향으로의 큰 속도 차이는 임펠러와 베인디퓨져 사이에서 유체의 혼합손실을 증가시키게 되며 이는 압축기 효율 감소로 이어진다. 따라서 최적화 임펠러의 공력손실 감소는 임펠러 출구에서의 더욱 균일한 속도분포에 기인한다.

Fig. 11

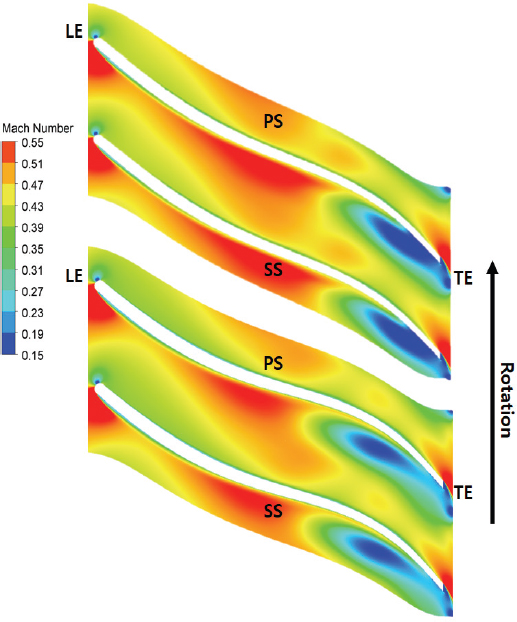
Mach number contours for the mid-span of the baseline impeller(top) and the optimized impeller(bottom)

최적화된 압축기의 임펠러 공력손실 분석을 위해 엔트로피 증가량을 분석하였다. Fig. 12는 압축기 임펠러 중간스팬에서 엔트로피 상승 값이다. 엔트로피 상승 값은 각 위치의 엔트로피 값에서 임펠러 입구 엔트로피값의 차이로 정의하였다. 높은 엔트로피 상승을 보이는 영역은 Fig. 11에서 나타난 낮은 유속 영역과 밀접한 관련을 보인다. 최적화된 압축기의 임펠러의 경우 기존 형상보다 엔트로피 상승량이 크게 감소하였다.

Fig. 12

Entropy contours of the mid-spans for the baseline(left) and optimized(right) impeller

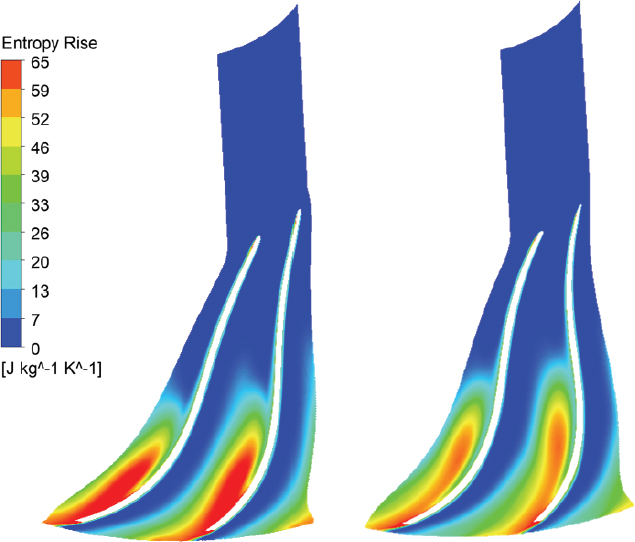
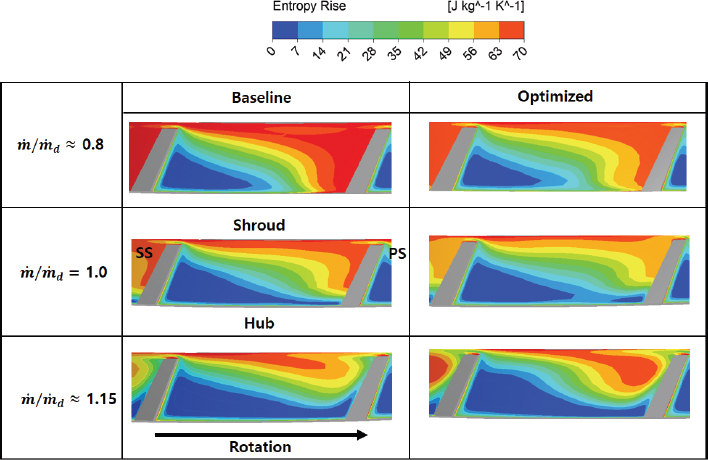
탈설계점 공력효율 변화 분석을 위해 임펠러 출구에서 엔트로피 상승량을 저유량($$ \dot{m}/{\dot{m}}_d$$≈0.8), 설계 유량($$ \dot{m}/{\dot{m}}_d$$=1) 및 고유량($$ \dot{m}/{\dot{m}}_d$$≈1.15) 조건에서 분석하였다(Fig. 13). 공통으로 임펠러 출구의 슈라우드 영역에서 높은 엔트로피 영역이 나타나며, 이는 팁 누설 유동에 기인한다. 저유량과 설계 유량 조건에서는 유로 개선 효과로 인하여 최적화된 압축기 임펠러의 출구에서 엔트로피 증가량이 감소하였다. 하지만 고유량 조건에서는 엔트로피 증가량이 기존 형상대비 최적화 형상에서 증가하였으며 이는 고유량 영역에서 등엔트로피효율 감소로 이어진다(Fig. 10(b)). 따라서 최적화 설계를 통해 도출된 압축기 입구부 유로 및 임펠러 형상 개선을 통해 유동특성이 개선되었다.

Fig. 13

Entropy contours for the impeller outlet planes baseline and optimized compressors

최적화된 베인 디퓨져의 성능을 분석하기 위해 정압력회복계수(static pressure recovery coefficient)를 분석하였다. 정압력회복계수는 디퓨져 입구에서의 운동에너지가 정압력으로 변환되는 비율을 나타내는 값으로 식(3)과 같이 정의된다⁽¹⁴⁾.

$\[ C{p}_{diffuser }=\frac{P_s-P_{s3}}{P_{t3}-P_{s3}} \]$

(3)

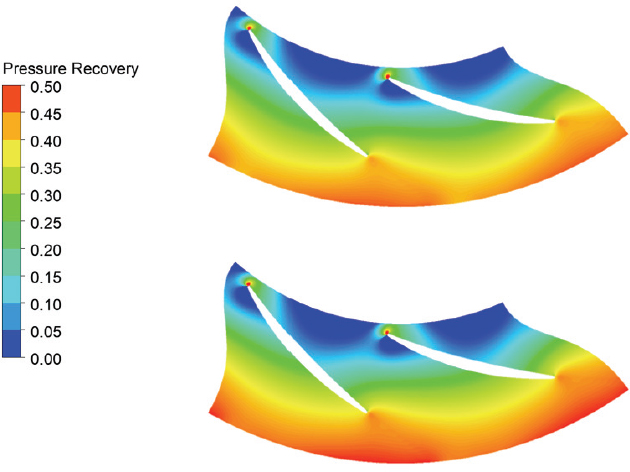
Fig. 14는 기존 및 최적화 형상의 베인 디퓨져 중간 스팬에서의 정압력회복계수 분포를 나타낸다. 기존 형상 대비 최적화된 베인 디퓨져는 블레이드 유로에서 더 높은 압력회복계수를 나타내며 디퓨져 출구에서 정압력이 더 높아지는 것을 알 수 있다. 따라서 최적화 절차를 통해 설계된 디퓨져형상 개선을 통해 유동의 운동에너지가 정압으로 더 많이 회복하였고 이는 압축기 등엔트로피 효율 향상으로 이어진다 (Fig. 10(b)).

Fig. 14

Diffuser inlet-to-outlet static pressure recovery coefficient contours at the diffuser mid-span for baseline(top) and optimized bottom compressors

5. 결 론

실제 산업에서 사용되고 있는 공기원심압축기의 임펠러 및 베인디퓨져 형상에 대한 최적화를 진행하였다. 최적화는 방사형 기저함수망을 적용한 대체모델을 기반으로 진행하였다. 이 과정에서 설계변수가 효율, 압력비 및 작동 범위에 미치는 영향을 분석하였으며, 성능 향상 원인을 밝히기 위해 상세한 유동 시뮬레이션을 수행하고, 초기 모델과 최적화된 모델에 대해 비교 분석하였다. 본 연구에서 얻은 결론은 다음과 같다.

• 1) 최적화된 압축기는 설계점 및 저유량 범위에서 약 2%의 등엔트로피 효율 향상을 보였으며 소요동력은 약 1∼4% 감소하였다. 설계유량 115% 이상 범위에서는 등엔트로피 효율 및 압력비가 감소하였다.
• 2) 설계 유량 조건에서 기존 형상대비 최적화된 원심압축기의 임펠러의 흡입면 측 TE부근의 저유속 영역이 작아졌으며 유동혼합손실 감소로 엔트로피 상승량이 크게 감소하였다. 저유량 조건에서는 유로 개선효과로 인하여 임펠러 출구 영역에서 팁유동에 의한 엔트로피 증가량이 감소하였으며 고유량 조건에서는 반대로 엔트로피 증가량이 증가하였다.
• 3) 베인디퓨져의 정압력회복 계수는 기존 형상 대비 최적화 형상에서 높게 나타났으며 이는 유동의 운동에너지가 정압력으로 변환되는 비율이 높아졌으며 디퓨져 유로에서의 공력손실 감소를 의미한다.
• 4) 본 연구를 통해 임펠러와 베인디퓨저를 동시에 최적화하여 기존 압축기 단열효율 대비 1.8% 향상을 달성하였으며 이를 통해 기존 압축기를 개보수하는 과정에 본 연구에서 제안한 방법을 적용할 수 있음을 보였다.

Acknowledgments

본 연구는 산업통상자원부와 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 ‘가변형 고효율 유체기기 핵심 기술 및 운영 시스템 개발’ 과제(No. 2021202080026C) 및 국토교통부/국토교통과학기술진흥원의 지원으로(과제번호 RS-2022-00143652) 수행된 연구결과이며, 이에 감사드립니다.

References

• Jeong, C., 2022, “The Use Status and the Efficent Use Plan of an Air Compressor,” MS. Thesis, Department of Smart Production and Management Engineering, Hanbat National University, Daejeon, Korea.
• Choi, H. J., Park, Y. H., Ahn, K. Y., & Cho, S. Y., 2011, “Optimization of a Centrifugal Compressor Impeller(I): Shape Parameters and Design Variables,” Journal of the Korean Society for Aeronautical, Vol. 39, No. 5, pp. 424∼432. [https://doi.org/10.5139/JKSAS.2011.39.5.424]
• Kim, S., Park, J., Ahn, K., Baek, J., 2010, “Numerical investigation and validation of the optimization of a centrifugal compressor using a response surface method,” Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy, Vol. 224, Issues 2, pp. 251∼ 259. [https://doi.org/10.1243/09576509JPE842]
• Bonaiuti, D., Arnone, A., Ermini, M., and Baldassarre, L., 2006, “Analysis and Optimization of Transonic Centrifugal Compressor Impellers Using the Design of Experiments Technique,” Journal of Turbomachinery, Vol. 128, No. 4, pp. 786∼797. [https://doi.org/10.1115/1.1579507]
• Seo, J., Park, J. Y., & Choi, B. S., 2014, “A Numerical Study on Shape Design Optimization for an Impeller of a Centrifugal Compressor,” The KSFM Journal of Fluid Machinery, Vol. 17(3), pp. 5-12. [https://doi.org/10.5293/kfma.2014.17.3.005]
• Ma, Y., Engeda, A., Cave, M., & Di Liberti, J.-L., 2010, “Improved centrifugal compressor impeller optimization with a radial basis function network and principle component analysis,” Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, Vol. 224, Issues 4, pp. 935∼945. [https://doi.org/10.1243/09544062JMES1635]
• Kim, J. H., Choi, J. H., and Kim, K. Y., 2010, “Surrogate Modeling for Optimization of a Centrifugal Compressor Impeller,” International Journal of Fluid Machinery and Systems, Vol. 3, No. 1, pp. 29∼38. [https://doi.org/10.5293/IJFMS.2010.3.1.029]
• Wang, X.-F., Xi, G., Wang, Z.-H., “Aerodynamic optimization design of centrifugal compressor's impeller with Kriging model,” Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy, Vol. 220, Issues 6, pp. 589∼597. [https://doi.org/10.1243/09576509JPE201]
• Faber, Vance & Gunzburger, Max., 1999, “Centroidal Voronoi Tessellations: Applications and Algorithms.” Siam Review - SIAM REV. 41. 637-676. [https://doi.org/10.1137/S0036144599352836]
• Saka, Y., Gunzburger, M., & Burkardt, J., 2007, “Latinized, improved LHS, and CVT point sets in hypercubes.” International Journal of Numerical Analysis and Modeling, 4(3-4), 729-743.
• Poggio, T., & Girosi, F., 1990, “Networks for Approximation and Learning.” Proceedings of the IEEE, 78(9), 1481–1497. [https://doi.org/10.1109/5.58326]
• P. A. Vikhar, 2016, "Evolutionary algorithms: A critical review and its future prospects," International Conference on Global Trends in Signal Processing, Information Computing and Communication, Jalgaon, India, pp. 261-265. [https://doi.org/10.1109/ICGTSPICC.2016.7955308]
• Slowik, A., & Kwasnicka, H., 2020, “Evolutionary algorithms and their applications to engineering problems.” Neural Comput & Applic Vol. 32, pp. 12363–12379. [https://doi.org/10.1007/s00521-020-04832-8]
• Rodgers, C., 1982. “The performance of centrifugal compressor channel diffusers.” In Turbo Expo: Power for Land, Sea, and Air, Vol. 79566, pp. V001T01A003. [https://doi.org/10.1115/82-GT-10]