[ Original Paper ]

The KSFM Journal of Fluid Machinery - Vol. 28, No. 2, pp.23-31

ISSN: 2287-9706 (Print)

Print publication date 01 Apr 2025

Received 24 Oct 2024 Revised 31 Dec 2024 Accepted 18 Jan 2025

DOI: https://doi.org/10.5293/kfma.2025.28.2.023

유동 조건에 따른 U자형 초음파 유량계 내부 공동현상에 관한 수치해석적 연구

김재현^* ; 김진영^* ; 최원우^* ; 김성민^**^{, †}

*성균관대학교 대학원 기계공학과
**성균관대학교 기계공학부

Numerical Study on Cavitation Inside a U-shaped Ultrasonic Flow Meter Under Various Flow Conditions

Jae-Hyun Kim^* ; Jin-Young Kim^* ; Won-Woo Choi^* ; Sung-Min Kim^**^{, †}

*Graduate School of Mechanical Engineering, Sungkyunkwan University
**School of Mechanical Engineering, Sungkyunkwan University

Correspondence to: ^†E-mail : smkim@skku.edu

Abstract

In this study, a three-dimensional numerical analysis of cavitation in a U-shaped ultrasonic flow meter was conducted under various flow conditions. Cavitation occurred near the outlet where the flow direction in the ultrasonic flow meter changed abruptly. The numerical analysis was performed for different outlet pressures, inlet flow rates, fluid temperatures, and working fluids. The results showed that the bubble generation area increased as the outlet pressure decreased and the inlet flow rate increased. Additionally, the flow and bubble generation characteristics inside the ultrasonic flow meter were influenced by fluid temperature and the type of working fluid due to changes in their thermophysical properties. The critical cavitation number, indicating the threshold for cavitation in the ultrasonic flow meter, was determined through numerical analysis.

Keywords:

Bubble formation, Computational fluid dynamics, Multiphase flow, Vapor volume fraction

키워드:

기포생성, 전산유체역학, 다상유동, 기체체적분율

1. 서 론

오늘날 반도체 제조, 화학 공정, 제약 산업 등 여러 산업 분야에서 기술이 발전함에 따라 정확한 유량 측정을 요구하고 있다⁽¹⁾. 특히, 다양한 액체 화학약품을 혼합하여 사용하는 반도체 세정 공정의 경우, 생산하는 반도체의 품질 관리를 위해 실리콘 웨이퍼에 공급되는 액체 화학약품의 양을 정밀하게 조절하기 위해 초음파 유량계를 사용하여 유량을 측정한다⁽²⁾. 반도체 세정 공정에 사용되는 초음파 유량계의 경우, 초음파가 전달되는 속도의 차이를 이용하여 유량을 측정한다. 두 개의 송⋅수신 트랜스듀서에서 발생한 초음파의 속도는 초음파 유량계 내 유속에 영향을 받기 때문에 유동 방향의 초음파는 유속만큼 빠르게 전달되고, 유동 반대 방향의 초음파는 유속만큼 느리게 전달된다. 따라서 속도가 다른 두 초음파가 트랜스듀서에 도달하는 시간차가 발생하고, 시간차와 초음파의 주파수를 사용하여 유량을 계산한다^(3–7). 하지만 초음파 유량계의 유량 측정 정확도는 상류의 불규칙한 흐름이나 유체 내 불순물 등에 의해 저하될 수 있다⁽⁸⁾. 유체 내 포함되어 있는 기포는 초음파 유량계의 정확도를 감소시키는 불순물 중 하나로, 초음파의 신호 전달을 방해하여 계측 오류를 발생시킬 수 있다⁽⁹⁾. 기포는 초음파 유량계 상류에서부터 유체에 함유되어 유입되기도 하지만, 초음파 유량계 내부에서 공동현상으로 인해 발생할 수 있다.

공동현상은 액체의 압력이 포화 압력 이하로 감소할 때, 온도 변화 없이도 상변화가 일어나 기포가 생성되는 현상이다⁽¹⁰⁾. 공동현상은 유로의 기하학적 형상이나 유동 조건 등 다양한 요인에 의해 발생하고 시스템 안정성에 큰 영향을 주기 때문에 관련된 연구가 활발히 진행되고 있다. 유로의 단면적이 축소했다가 확장하는 과정에서 속도 및 압력 변화가 급격히 발생하는 벤츄리 노즐이나 압력 차가 발생하는 유체 기계 날개 등을 대상으로 다양한 연구가 이루어지고 있다^(11–15).

이외에도 유동 방향이 급격히 변하는 유로 형상에서 발생하는 공동현상에 대한 연구가 진행되고 있다. Yousaf⁽¹⁶⁾ 등은 다양한 곡률 반경을 가진 엘보우 파이프에서 발생하는 공동현상에 대해 분석함으로써 엘보우 곡률이 감소함에 따라 엘보우 근처에서 공동현상이 활발히 발생함을 확인하였다. Chang⁽¹⁷⁾ 등은 엘보우 파이프에서 입구 속도, 출구 압력, 그리고 엘보우 파이프 각도가 액체 수소의 공동현상에 미치는 영향에 대해 수치해석적 연구를 진행하였다. 공동현상은 입구 속도 및 출구 압력의 변화에 큰 영향을 받아 입구 속도가 증가하거나 출구 압력이 감소함에 따라 공동현상이 넓은 영역에서 발생하였고, 엘보우 각도가 감소하면서 공동현상이 강하게 발생함을 보였다. 이전의 연구들에서 다양한 유체 기계에서 발생하는 공동현상에 관한 연구가 수행되었고, 본 연구에서는 초음파 유량계 내에서 발생하는 공동현상을 대상으로 연구를 진행하였다.

본 연구에서는 반도체 세정 공정에 사용되는 U자 형태의 초음파 유량계에 대해 출구 압력, 입구 유속, 유체 온도, 그리고 작동유체의 종류에 따른 초음파 유량계 내부 공동현상 발생을 확인하였다. 3차원 수치해석을 진행하였고 다양한 유동 조건 및 작동유체의 변화가 공동현상에 미치는 영향을 확인하여 공동현상이 발생하지 않는 유동 조건에 대한 분석을 진행하였다.

2. 수치해석

2.1 수치해석 형상 및 경계조건

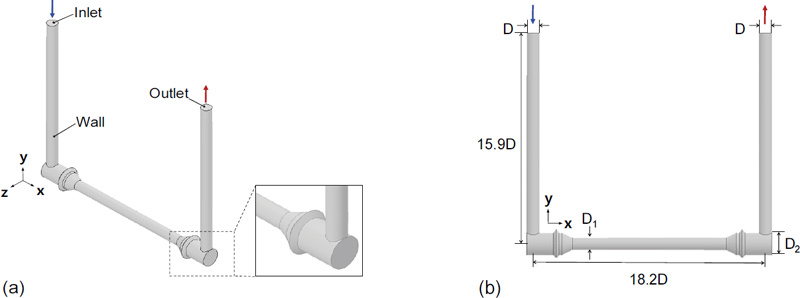
Fig. 1(a)는 본 연구에서 사용한 U자형 초음파 유량계를 등축 투영한 그림이다. x축과 평행한 배관체의 양 끝에 y축과 평행한 두 배관체가 수직으로 접합되어 있는 좌우 대칭 형태로, y축 방향의 배관체를 통해 작동유체가 유입되어 반대쪽 평행한 배관체를 통해 유출된다. Fig. 1(b)와 같이 y축과 평행한 두 배관체와, 그들과 접합한 배관체의 직경은 각각 D와 D₁으로 설정하였다. 배관체 접합부 인근 직경은 D₂로 설정하여 x축과 평행한 배관체 유로 단면적의 축소 및 확대가 발생한다. 배관체 직경비 D₁/D과 D₂/D는 각각 0.95와 1.68로 설정하였다. 초음파 유량계의 길이는 입구 직경 비로 표현되며, 초음파 유량계 입구부터 x축과 평행한 배관체 중심축까지 길이는 15.9D, y축과 평행한 배관체 중심축 사이의 길이는 18.2D이다.

Fig. 1

(a) Isometric and (b) xy-plane view of ultrasonic flow meter

초음파 유량계 입구에는 속도와 온도 경계조건, 출구에는 압력 경계조건을 부여하였고, 초음파 유량계의 모든 벽면 경계에서는 점착 조건(No slip condition)과 단열을 가정하여 해석 영역을 구축하였다.

본 연구에서는 유동 조건 및 작동유체의 변화가 초음파 유량계 내 공동현상에 미치는 영향에 대해 파악하기 위해 다양한 출구 압력, 입구 유량, 유체 온도, 그리고 작동유체에 대하여 3차원 수치해석을 진행하였다. 압력, 유량, 온도 조건은 각각 P/P_ref, Q/Q_ref, 그리고 T/T_ref와 같이 참조 값과의 비를 통해 무차원 형태로 표시하였다. 또한, 유속, 밀도, 압력으로 계산되는 캐비테이션 수를 활용하여 정량적으로 공동현상이 발생하는 정도를 비교하였다. 캐비테이션 수는 다음과 같이 정의하였다.

σ = P - P v 12 ρ U 2

(1)

이때 P는 출구 압력을, P_v는 특정 온도에서 유체의 포화 압력을 나타낸다. ρ, U는 각각 초음파 유량계 입구에서의 액체 밀도와 유속을 나타낸다. 본 연구에서 총 41개의 케이스에 대한 수치해석을 진행하였고 Table 1에 정리하였다. 작동유체의 경우, 유체의 물리적 특성이 공동현상에 미치는 영향을 분석하기 위해 물리적 특성이 서로 다른 물, 아세톤, 그리고 50/50 EGW를 작동유체로 선정하였다. 작동유체의 밀도 및 점도와 같은 물성치는 NIST의 REFPROP 9.1⁽¹⁸⁾ 프로그램을 사용하여 얻었다. 관련된 작동유체의 물성치는 Table 2에 정리하였다.

Table 1

Flow parameters for all 41 cases with different working fluids

Table 2

Thermophysical properties of water, acetone, and 50/50 EGW at saturation pressure for T/Tref = 3

2.2 지배방정식

액체와 기체 상변화 현상을 해석하기 위한 다상 모델로 Mixture 모델을 사용하였다. Mixture 모델은 기체 기포가 유체 내 균일하게 분산된 것으로 가정하며, 분산된 기포들을 연속체로 취급하여 개별적으로 추적하지 않는다. 다수의 기포로 구성된 단순화된 기포 생성영역을 계산하기 때문에 계산 비용을 절약함과 동시에 정확한 해석 결과를 얻을 수 있다⁽¹⁹⁾. Mixture 모델에 대한 정상상태 연속 방정식은 다음과 같이 나타낼 수 있다.

∇ ⋅ ρ m v m → = 0

(2)

v m → = ∑ k = 1 2 α k ρ k v k → ρ m

(3)

ρ m = ∑ k = 1 2 α k ρ k

(4)

이때, m과 k는 각각 혼합 유체와 유체 내 존재하는 유체의 상을 의미하며, 1번째 유체는 액체 상, 2번째 유체는 기체상으로 설정하였다. $v m →$ 과 ρ_m은 각각 질량 평균 속도와 혼합물의 밀도를 나타내고 α_k는 유체의 상에 대한 체적분율을 나타낸다.

다상 유동의 운동량 방정식은 다음과 같이 나타낼 수 있다.

∇ ⋅ ρ m v m → v m → = - ∇ P + ∇ ⋅ μ m ∇ v m → + v m T → + F →

(5)

μ m = ∑ k = 1 2 α k μ k

(6)

이때, $F →$ 과 μ_m은 각각 체적 힘과 혼합물의 점도를 나타낸다.

2.3 공동 모델

공동현상을 해석하기 위해 Rayleigh-Plesset 기포 성장 방정식을 적용하였다. 기포의 성장과 붕괴 과정을 설명하는 Rayleigh-Plesset 기포 성장 방정식은 다음과 같이 나타낼 수 있다⁽¹⁹⁾.

P B t - P ∞ t ρ l = R B d 2 R B d t + 32 d R B d t 2 + 4 v l R B d R B d t + 2 γ ρ l R B

(7)

여기서 하첨자 l은 액체상을 나타내고, P_B는 기포의 압력, R_B와 γ는 각각 기포의 반경과 표면 장력을 나타낸다. 열적 효과와 2차 항, 그리고 표면 장력을 무시한다면 식 (7)은 다음과 같이 나타낼 수 있다.

d R B d t = 2 P B - P 3 ρ l

(8)

단위 부피당 기포의 생성과 붕괴를 계산하기 위한 공동 모델로 Zwart-Gerber-Belamri 모델을 사용하였다. Zwart-Gerber-Belamri 모델은 시스템의 모든 기포가 동일한 크기를 가진다고 가정하고, 단위 부피당 총 계면 물질 전달 속도를 기포 수 밀도와 단일 기포의 질량 변화율을 사용하여 계산한다^(20–21). 위 모델을 활용해 순 질량 전달량 R을 식 (9)와 같이 표현할 수 있고, 기포의 압력을 기준으로 액체에서 기체로의 질량 전달률은 식 (10), 기체에서 액체로의 질량 전달률은 식 (11)과 같이 나타낼 수 있다.

R = 3 α ρ v R B 2 P B - P 3 ρ l

(9)

R e = F v a p 3 α n u c 1 - α v ρ v R B 2 P B - P 3 ρ l

(10)

R c = F c o n d 3 α v ρ v R B 2 P - P B 3 ρ l

(11)

∂ α v ρ v ∂ t + ∂ ρ v α v U i v ∂ x j = R e - R c

(12)

이때 하첨자 v는 기체상을 의미한다. α_nuc, F_vap, 그리고 F_cond는 각각 핵 사이트 체적분율(nucleation site volume fraction)과 증발 및 응축 계수를 나타낸다. Zwart-Gerber-Belamri 모델의 파라미터 R_B, α_nuc, F_vap, 그리고 Fcond는 Zwart⁽²⁰⁾ 등이 제시한 상수를 사용하였다(R_B = 10^-6 m, α_nuc = 5×10^-4, F_vap = 50, F_cond = 0.01). 식 (10)과 식 (11)을 통해 계산된 질량 전달률은 식 (12)와 같이 표현되는 물질 전달 방정식의 소스 항으로 계산된다.

2.4 수치해석 기법

본 연구에서는 상용 전산유체역학 소프트웨어인 ANSYS Fluent 20.1⁽²⁰⁾을 사용하여 3차원 정상상태 해석을 수행하였다. Realizable k-ε 난류 모델을 사용하여 유동해석을 수행하였고, 압력-속도 연성을 위하여 Semi-implicit method for pressure linked equations(SIMPLE)⁽²³⁾기법을 사용하였다. PREssure STaggering Option(PRESTO)⁽²⁰⁾을 사용하여 압력을 보정하고, 운동량과 난류운동에너지의 이산화에는 Second order upwind를 사용하였고, 이외 나머지는 First order upwind를 사용하였다.

2.5 수치해석 격자 독립성 검증

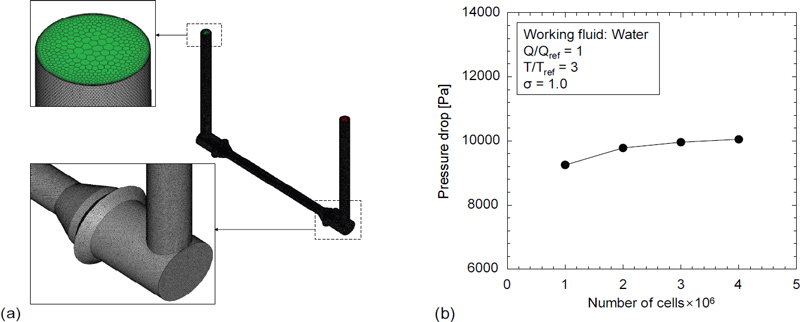
초음파 유량계 형상에 대하여 0.97×10⁶, 1.99×10⁶, 3.05×10⁶, 4.02×10⁶개의 격자를 가지는 격자 시스템에 대하여 격자 독립성 검증을 수행하였다. Fig. 2(a)와 같이 격자 시스템은 Polyhedral 격자로 구성하였고, 수치해석 결과의 정확성과 수렴성 향상을 위해 벽 근처에 조밀한 격자를 생성하였다. 4가지 격자 시스템에 대하여 초음파 유량계 입출구 압력강하를 비교하였고, 비교 결과는 Fig. 2(b)에 나타냈다. 그래프에서 확인할 수 있듯이 3.05×10⁶개와 4.02×10⁶개의 격자를 가지는 시스템의 입출구 압력강하 차이가 1.32%로 나타나 3.05×10⁶개의 격자 시스템을 수치해석 모델로 선정하였다.

Fig. 2

(a) Grid system comprising 3.05 million polyhedral cells and (b) grid independence test by comparing total pressure drop

3. 수치해석 결과

Fig. 3은 물을 작동유체로 하고 Q/Q_ref = 1, T/T_ref = 3, 그리고 σ = 1일 때 초음파 유량계 내 속도 분포를 보여준다. 초음파 유량계에 유입된 유체는 x축과 평행한 배관체 벽과 충돌하며, 충돌 후 Fig. 3(b)의 x = D₂ 단면적 속도 분포와 같이 복잡한 유동장이 형성되었다. 이후 초음파 유량계 내 x축 방향으로 와류 유동이 발달하였다. 출구와 인접한 배관체 접합부에서는 유동의 방향이 급격히 변하면서 y = D₂/2 단면에서 불균일한 유동이 발생하였다. 또한, 초음파 유량계 입구와 x축 거리가 가까운 배관체 벽 인근에서 상대적으로 높은 유속이 관측되었다. 이후 y축 방향으로 유동이 발달함에 따라 유동 불균일이 해소되었다. Fig. 4(a)는 Fig. 3와 동일한 유동 조건에서 압력 분포를 나타낸다. x축과 평행한 배관체의 단면적이 축소되는 부분에서 압력강하가 발생하고, 단면적이 확대되면서 국부적으로 압력강하가 발생하는 부분이 관찰되지만, 유로 팽창으로 인해 압력이 회복되었다. 출구와 인접한 배관체 접합부에서는 유동 방향이 급격하게 변하면서 국부적으로 큰 압력강하가 발생하였다. y = D₂/2 단면에서 가장 높은 속도를 보인 입구와 거리가 가까운 배관체 벽 주변에서는 압력이 포화 압력까지 감소하고 공동현상이 발생하였다. Fig. 4(b)는 기체 체적분율(vapor volume fraction)이 0.1인 영역을 보여준다. 기체 체적분율 0.1 미만인 구간은 공동이 희박하게 형성되는 구간으로, 수치해석 상에서 기체 체적분율 0.1 이상인 구간부터 기포 생성영역으로 판단하였다⁽²²⁾. 이때 기포 생성영역의 부피는 0.52 mm³로 나타났다. 그림에서 보이는 것과 같이, 포화 압력까지 압력강하가 발생한 구간에서 공동이 발생하였고, x축과 평행한 배관체에서 발달한 와류 유동으로 인해 Fig. 4(b)와 같은 형태의 기포 생성영역이 나타났다. y축 방향으로 유동이 진행되면서 배관체 단면 내 유동 불균일이 해소되었고, 압력이 회복되면서 기포 생성영역이 감소하는 모습을 보였다.

Fig. 3

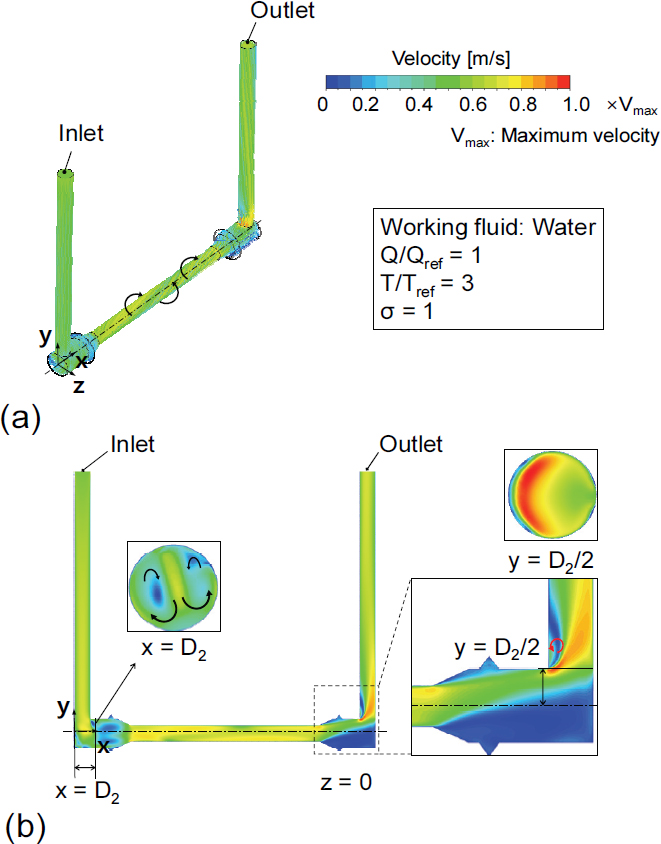
(a) Three-dimensional velocity streamline and (b) velocity contours on xy-plane at Q/Qref = 1, T/Tref = 3, and σ = 1 using water

Fig. 4

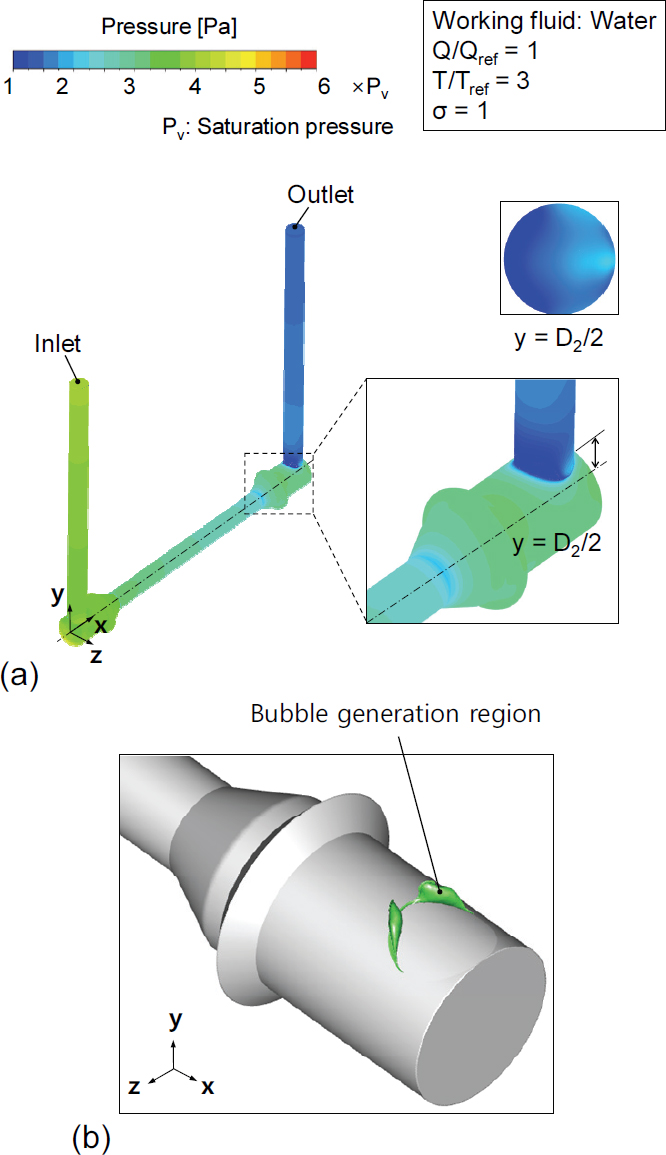
(a) Pressure distributions and (b) isosurface of bubble generation region at Q/Qref = 1, T/Tref = 3, and σ = 1 using water

3.1 출구 압력의 효과

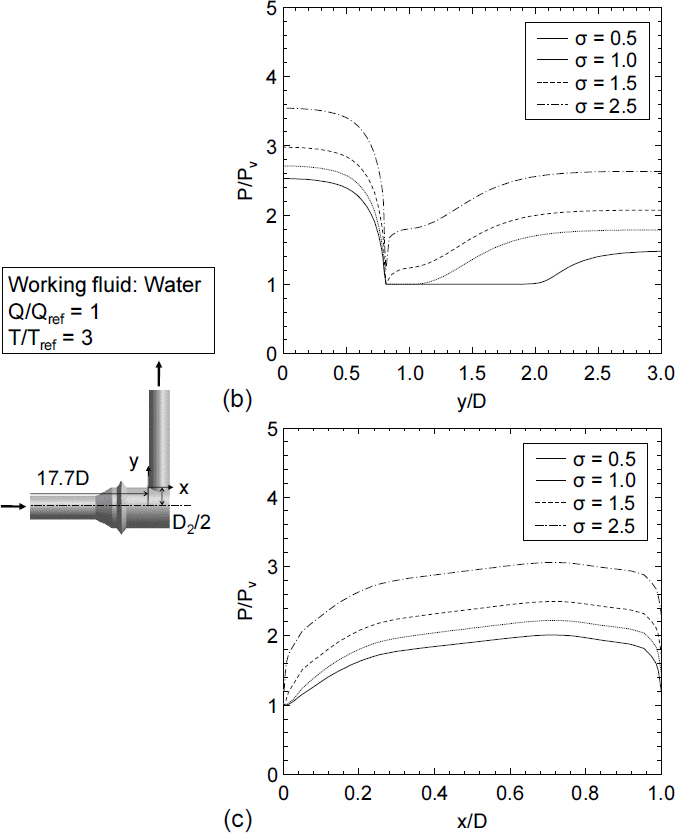
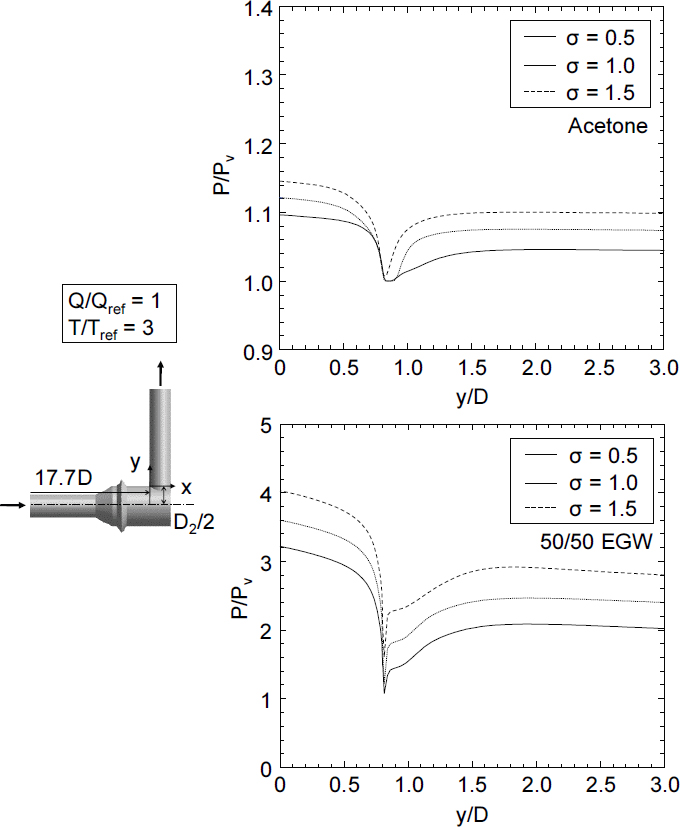
Fig. 5(a)는 작동유체를 물로 설정하고 Q/Q_ref = 1, T/T_ref = 3일 때 다양한 출구 압력에 따른 출구와 인접한 배관체 접합부에서의 기포 생성영역을 보여준다. 출구 압력을 제외한 다른 유동 조건은 고정되었기 때문에 캐비테이션 수는 출구 압력에 의해서만 변화하고, 출구 압력이 감소할수록 캐비테이션 수는 감소한다. 출구 압력이 가장 낮은 σ = 0.5일 때 가장 넓은 영역에서 기포가 생성되었고, y축 방향으로 길게 기포 생성영역이 전개되었다. 반면, 출구 압력이 증가하여 캐비테이션 수가 증가하는 경우에는 기포 생성영역이 크게 감소하였고, y축 방향으로 기포 생성영역의 길이가 감소함을 보였다. 하지만 캐비테이션 수가 0.5–2.5인 구간에서 공동현상은 동일하게 배관체가 접합하는 경계면에서 발생하기 시작하였는데, 이는 접합부의 기하학적 특성이 공동 발생에 미치는 영향이 크기 때문에 동일한 위치에서 공동이 발생하기 시작한 것으로 판단할 수 있다. 하지만 출구 압력이 증가하여 σ > 2.5인 경우에는 공동현상이 관측되지 않았다. Fig. 5(b)는 기포 생성영역이 관측되는 출구와 인접한 배관체 접합부의 입구와 거리가 가까운 배관체 벽에서 y축 방향 압력 분포를 나타낸 것이다. y축은 국부 압력과 포화 압력의 비로, P/P_v = 1일 때는 국부 압력이 포화 압력과 같아져 공동이 발생함을 의미한다. 캐비테이션 수가 감소할수록 P/P_v = 1인 구간이 y축 방향으로 길게 나타나는 모습을 보였다. Fig. 5(c)는 y = D₂/2 배관체 단면에서의 반지름 방향 압력비를 나타낸 그림이다. 캐비테이션 수가 감소할수록 단면 내 x/D = 0 인근에서 기울기가 완만함을 보여주는데, 이는 출구 압력이 감소할수록 유동 방향뿐만 아니라 반지름 방향을 따라 기포 생성영역이 두껍게 형성됨을 보여준다.

Fig. 5

(a) Isosurface of bubble generation region at Q/Qref = 1 and T/Tref = 3 for different cavitation numbers. Pressure distributions at Q/Qref = 1 and T/Tref = 3 for different cavitation numbers along (b) axial direction and (c) radial direction using water

3.2 입구 유량의 효과

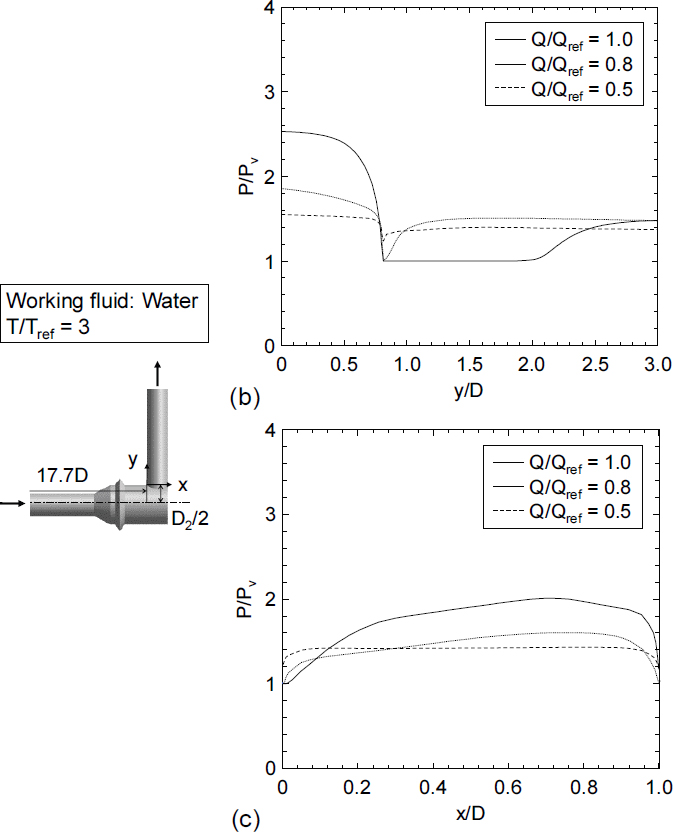
입구 유량이 공동현상에 미치는 영향을 파악하기 위해 동일한 출구 압력과 유체 온도에서 유체의 입구 유속을 변화시키며 기포 생성영역을 비교하였다. Fig. 6(a)는 물을 작동유체로 사용하고 T/T_ref = 3일 때 유속에 따른 기포 생성영역을 나타내는 그림이다. 유량비 0.8의 경우, 유량비가 1인 경우와 비교했을 때 기포 생성영역은 크게 감소하였다. 유량비 0.5인 경우에는 기포 생성영역이 거의 발생하지 않음을 보였다. Fig. 6(b)는 Fig. 5(b)와 동일한 영역에서의 y축 방향 압력 분포를 나타내는데, 유량이 감소함에 따라 P/P_v = 1인 구간이 급격히 감소하는 모습을 보였다. 또한, 유량이 감소할수록 급격한 압력강하 이후 빠른 압력 회복을 보였다. Fig. 6(c)는 Fig. 5(c)와 동일한 영역에서 반지름 방향 압력 분포를 나타낸 것으로, 유량이 감소함에 따라 단면 내 압력이 균일해짐을 보였다. 결과적으로 입구 유량이 감소함에 따라 출구와 인접한 배관체 접합부에서 기하학적 요인으로 인해 유동 방향이 급격히 변하더라도 최대 속도가 상대적으로 작게 나타나고, 공동현상이 발생하는 구간의 배관체 단면 내 유동이 균일해짐에 따라 기포 생성영역이 현저히 감소하였다.

Fig. 6

(a) Isosurface of bubble generation region at T/Tref = 3 for different flow rates. Pressure distributions at T/Tref = 3 for different flow rates along (b) axial direction and (c) radial direction using water

3.3 유체 온도의 효과

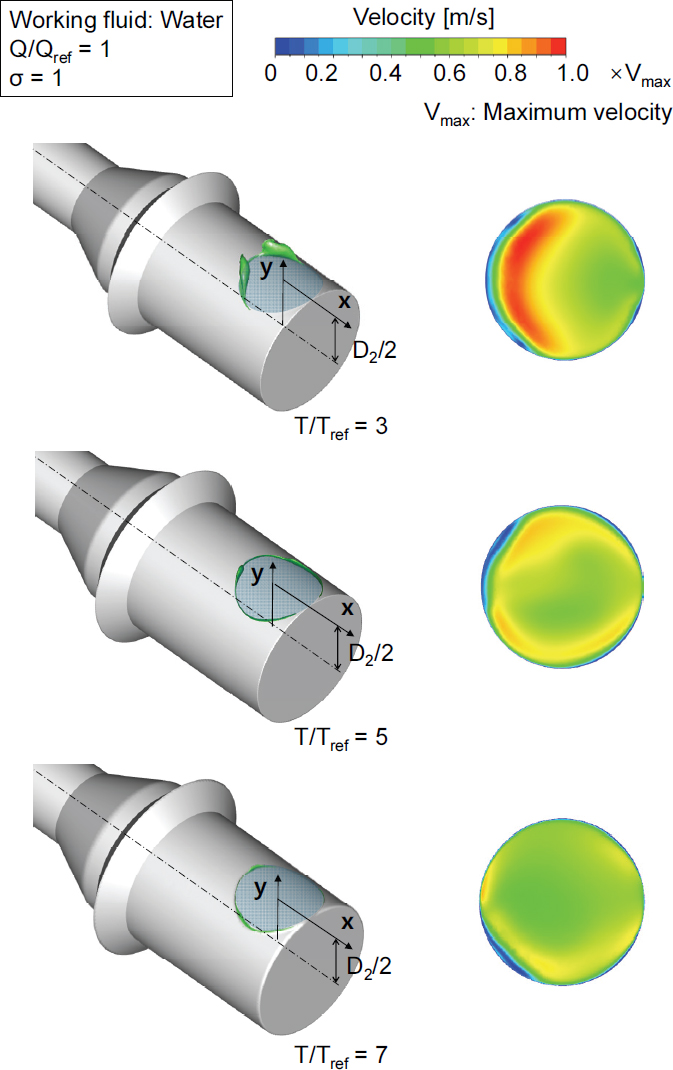
Fig. 7은 작동유체를 물로 설정하고 Q/Q_ref = 1, σ = 1일 때 다양한 유체 온도에 따른 출구와 인접한 배관체 접합부에서의 기포 생성영역과 y = D₂/2 배관체 단면 속도 분포를 나타낸 그림이다. 유체 온도에 따라 작동유체의 포화 압력이 변하기 때문에 동일한 캐비테이션 수에 대해 비교하였다. y = D₂/2 배관체 단면에서의 온도에 따른 속도 분포를 보면, T/T_ref = 7일 때 액체상의 물의 밀도와 점성이 감소하여 x축과 평행한 배관체 내 유체가 배관체 접합부 벽면에 충돌 후 최대 속도가 감소하고 상대적으로 균일한 속도 분포가 나타났다. 출구와 인접한 배관체 접합부에서의 기포 생성영역을 보면, T/T_ref가 5 이상일 때 배관체 접합부 경계를 따라 긴 기포 생성영역이 형성되었다. T/T_ref가 3에서 5로 증가할 때 유동 균일성이 크게 향상되고, 물성치 변화로 인한 기포 생성영역의 차이가 발생하였지만, T/T_ref가 5에서 7로 증가할 때, 유체 온도 증가로 인한 기포 생성영역의 차이는 비교적 미미하였다.

Fig. 7

Comparison of isosurfce of bubble generation regions and velocity distributions on y = D2/2 at Q/Qref = 1 and σ = 1 for different fluid temperatures using water

3.4 작동유체의 효과

작동유체가 공동현상에 미치는 영향을 분석하기 위해 아세톤과 50/50 EGW를 작동유체로 사용하여 수치해석을 진행하였다. Fig. 8은 아세톤과 50/50 EGW를 작동유체로 사용하였을 때 공동이 발생하는 출구와 인접한 배관체 접합부에서의 z = 0 단면 속도 분포 및 기포 생성영역을 나타낸다. Fig. 8에서 물에 비해 밀도와 점도가 작은 아세톤의 경우, 출구와 인접한 배관체 접합부에서 상대적으로 균일한 속도 분포를 보였고, 유동 방향이 급격히 변하는 구간에서 상대적으로 높은 속도가 관측되었다. Fig. 9는 기포 생성영역이 관측되는 출구와 인접한 배관체 접합부의 입구와 가까운 배관체 벽에서 y축 방향 압력 분포를 나타낸다. 작동유체로 아세톤을 사용했을 때 y축 방향을 따라 압력강하가 비교적 작게 나타났다. 50/50 EGW의 경우, Fig. 8의 z = 0 단면 속도 분포에 나타난 것과 같이 상대적으로 높은 점도로 인해 유동 방향이 변하는 구간에서 낮은 최대 속도를 보였다. 또한, Fig. 9의 y축 방향 압력 분포 그래프에 나타난 것과 같이 상대적으로 y축 방향으로 압력강하가 컸지만, P/P_v = 1인 구간이 짧게 나타났다. Fig. 8의 기포 생성영역을 비교했을 때, 아세톤의 경우 50/50 EGW에 비해 배관체 접합부 경계를 따라 긴 기포 생성영역이 나타났다. 동일한 유동 조건에서 물의 기포 생성영역과 비교했을 때, 아세톤과 50/50 EGW 모두 물성치 차이와 그로 인한 초음파 유량계 내 유동 발달 차이로 y축 방향으로 기포 생성영역이 짧게 형성되었다.

Fig. 8

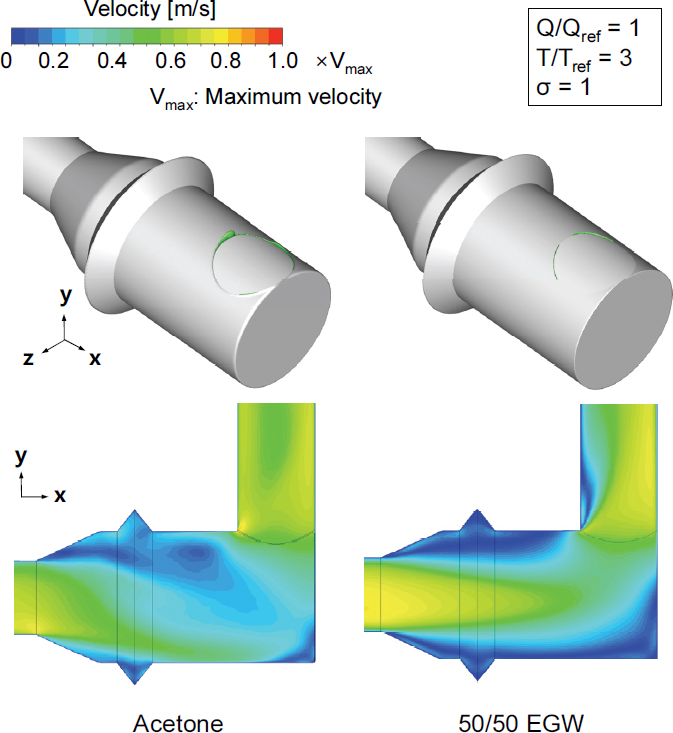
Comparison of isosurface of bubble generation regions and velocity distributions on xy-plane at Q/Qref = 1, T/Tref = 3, and σ = 1 using acetone and 50/50 EGW

Fig. 9

Pressure distributions along axial direction at Q/Qref = 1 and T/Tref = 3 using acetone and 50/50 EGW

3.5 기포 생성영역 비교

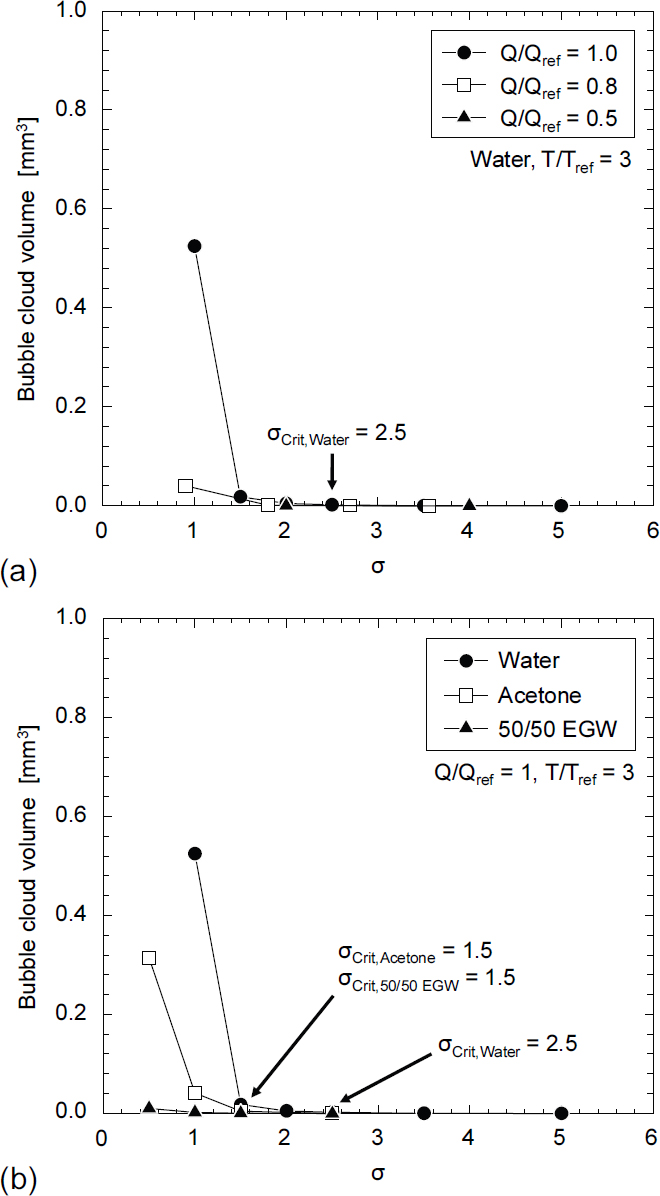
Fig. 10은 캐비테이션 수에 따른 기포 생성영역의 부피를 나타낸 그래프이다. σ_crit는 공동현상이 발생하기 시작하는 작동 조건을 나타내는 캐비테이션 수로, 캐비테이션 수가 σ_crit 보다 작으면 기포가 생성된다. Fig. 10(a)는 작동유체가 물, T/T_ref = 3일 때 캐비테이션 수에 따른 기포 생성영역의 부피를 나타낸다. 입구 유량이 증가할수록 σ < 1.5에서 캐비테이션 수가 증가함에 따라 기포 생성영역의 부피가 크게 감소함을 보였다. 또한, 입구 유량에 관계없이 σ > 2.5에서 기포가 생성되지 않았다. Fig. 10(b)는 작동유체 별 캐비테이션 수에 따른 기포 생성영역의 부피를 나타낸다. 아세톤의 경우, σ < 1.5에서 캐비테이션 수가 증가함에 따라 기포 생성영역의 부피가 크게 감소함을 보였다. 50/50 EGW의 경우, 캐비테이션 수에 따른 기포 생성영역의 부피 변화가 상대적으로 작게 나타났다. 아세톤과 50/50 EGW의 물성치 차이가 있음에도 동일하게 σ > 1.5에서 기포가 생성되지 않았다.

Fig. 10

Effect of cavitation number on bubble cloud volume (a) for different flow rates and (b) different working fluids

4. 결 론

본 연구에서는 물성치가 서로 다른 다양한 작동유체를 사용하여 출구 압력, 입구 유량, 그리고 유체 온도에 따른 초음파 유량계 내부 공동현상에 대한 수치해석을 수행하였다. 총 41개의 케이스에 대한 수치해석 결과를 요약하면 다음과 같다.

1) U자형 초음파 유량계에서 출구와 인접한 배관체 접합부의 기하학적 요인으로 인해 급격한 유속 증가와 압력강하가 크게 발생하면서 기포 생성영역이 나타났고, 유동 방향을 따라 압력이 회복되면서 기포 생성영역이 사라졌다.
2) 출구 압력이 감소함에 따라 기포 생성영역이 크게 형성되고, 입구 유량이 감소함에 따라 기포 생성영역이 감소하였다. 또한, 입구 유량이 감소함에 따라 배관체 단면 내 균일한 유동이 발생하고 압력강하가 감소하였다.
3) 유체의 온도가 상승함에 따라 물의 밀도와 점도가 감소하기 때문에 공동이 발생하는 부분에서 균일한 유동이 관측되었고, 배관체 접합부 경계를 따라 길게 기포 생성영역이 나타났다. 이러한 유체 온도의 영향은 T/T_ref가 5 이하일 때 두드러지게 관측되었다.
4) 작동유체에 따라 공동이 발생하는 부분에서의 유동 양상 및 압력 분포가 다르게 나타나고, 이로 인해 기포 생성영역의 차이가 발생하였다. 결과적으로 T/T_ref = 3일 때, 물, 아세톤 그리고 50/50 EGW는 각각 σ > 2.5, σ > 1.5 그리고 σ > 1.5에서 공동현상이 발생하지 않았다.

Acknowledgments

본 연구는 2023년 세메스 전략산학과제의 지원을 받아 수행된 연구임.

References

Chen, C., Sun, W., Zhou, R., Lin, C., Chu, C., and Su, S., 2024, “Optimization design and research of ultrasonic flowmeter based on time difference method,” Journal of Mechanical Science and Technology, Vol. 38, No. 1, pp. 245∼258. [https://doi.org/10.1007/s12206-023-1221-z]
Bae, I. J. and Lee, E. S., 2019, “Improvement of Measuring Stability of Amplitude Attenuation by the Bubble in Ultrasonic Flow-Meter for Semiconductor Process,” Journal Korean Society for Precision Engineering, Vol. 36, No. 9, pp. 843∼849. [https://doi.org/10.7736/KSPE.2019.36.9.843]
Rajita, G., and Mandal, N., 2016, “Review on transit time ultrasonic flowmeter,” 2016 2nd International Conference on Control, Instrumentation, Energy & Communication (CIEC). IEEE, pp. 88∼92. [https://doi.org/10.1109/CIEC.2016.7513740]
Comes, M., Drumea, P., Blejan, M., Dutu, I., and Vasile, A., 2006, “Ultrasonic flowmeter,” 2006 29th International Spring Seminar on Electronics Technology. IEEE, pp. 386 ∼389. [https://doi.org/10.1109/ISSE.2006.365135]
Ren, R., Wang, H., Sun, X., and Quan, H., 2022, “Design and implementation of an ultrasonic flowmeter based on the cross-correlation method,” Sensors, Vol. 22, No. 19, p. 7470. [https://doi.org/10.3390/s22197470]
Afandi, A., Catrawedarma, I. G. N. B., and Wijayanta, S., 2024, “The development of the ultrasonic flowmeter sensors for mass flow rate measurement: A comprehensive review,” Flow Measurement and Instrumentation, Vol. 97, p. 102614. [https://doi.org/10.1016/j.flowmeasinst.2024.102614]
Gao, Y., Chen, M., Wu, Z., Yao, L., Tong, Z., Zhang, S., Gu, Y. A., and Lou, L., 2023, “A miniaturized transit-time ultrasonic flowmeter based on ScAlN piezoelectric micromachined ultrasonic transducers for small-diameter applications,” Microsystems & Nanoengineering, Vol. 9, No. 1, p. 49. [https://doi.org/10.1038/s41378-023-00518-y]
Conrad, K., and Lynnworth, L., 2002, “Fundamentals of ultrasonic flow meters,” American School of Gas Measurement Technology, Vol. 1, pp. 53∼54.
Masasi, B., Frazier, R. S., and Taghvaeian, S., 2017, “Review and operational guidelines for portable ultrasonic flowmeters,” Oklahoma Cooperative Extension Service.
Franc, J. P., and Michel, J. M., 2006, “Fundamentals of cavitation,” Springer science & Business media, Vol. 76. [https://doi.org/10.1007/1-4020-2233-6]
Franc, J. P., 2007, “The Rayleigh-Plesset equation: a simple and powerful tool to understand various aspects of cavitation,” Fluid dynamics of cavitation and cavitating turbopumps. Vienna: Springer Vienna, pp. 1∼41. [https://doi.org/10.1007/978-3-211-76669-9_1]
Gu, Y., Zhang, J., Yu, S., Mou, C., Li, Z., He, C., Wu, D., Mou, J., and Ren, Yun., 2022, “Unsteady numerical simulation method of hydrofoil surface cavitation,” International Journal of Mechanical Sciences, Vol. 228, p. 107490. [https://doi.org/10.1016/j.ijmecsci.2022.107490]
Zhou, L., and Wang, Z., 2008, “Numerical simulation of cavitation around a hydrofoil and evaluation of a RNG κ -ε model,” Journal of Fluids Engineering, Vol. 130, No. 1, p. 011302. [https://doi.org/10.1115/1.2816009]
Tomov, P., Khelladi, S., Ravelet, F., Sarraf, C., Bakir, F., and Vertenoeuil, P., 2016, “Experimental study of aerated cavitation in a horizontal venturi nozzle,” Experimental Thermal and Fluid Science, Vol. 70, pp. 85∼95. [https://doi.org/10.1016/j.expthermflusci.2015.08.018]
Li, M., Bussonnière, A., Bronson, M., Xu, Z., and Liu, Q., 2019, “Study of Venturi tube geometry on the hydrodynamic cavitation for the generation of microbubbles,” Minerals Engineering, Vol. 132, pp. 268∼274. [https://doi.org/10.1016/j.mineng.2018.11.001]
Yousaf, B., Manzoor, T., Qaisrani, M. A., Khan, I., Sahar, M. S. U., and Tahir, W., 2022, “Investigation of influence of elbow on pump inlet flow behaviour in cavitating flow,” Engineering Failure Analysis, Vol. 137, p. 106420. [https://doi.org/10.1016/j.engfailanal.2022.106420]
Chang, H., Xie, X., Zheng, Y., and Shu, S., 2017, “Numerical study on the cavitating flow in liquid hydrogen through elbow pipes with a simplified cavitation model,” International Journal of Hydrogen Energy, Vol. 42, No. 29, pp. 18325∼18332. [https://doi.org/10.1016/j.ijhydene.2017.04.132]
Lemmon, E. W., Bell, I. H., Huber, M. L., and McLinden, M. O., 2018, “Reference Fluid Thermodynamic and Transport Properties-REFPROP, Version 10.0,” National Institute of Standards and Technology, Standard Reference Database 23.
Deng, S. S., Li, G. D., Guan, J. F., Chen, X. C., and Liu, L. X., 2019, “Numerical study of cavitation in centrifugal pump conveying different liquid materials,” Results in Physics, Vol. 12, pp. 1834∼1839. [https://doi.org/10.1016/j.rinp.2019.02.009]
ANSYS Inc., ANSYS Fluent Theory Guide, Canons burg, PA: release 20.1, 2019.
Zwart, P. J., Gerber, A. G., and Belamri, T., 2004, “A two-phase flow model for predicting cavitation dynamics,” Fifth international conference on multiphase flow. Japan: Yokohama, Vol. 152.
Yaghoubi, H., Madani, S. A. H., and Alizadeh, M., 2018, “Numerical study on cavitation in a globe control valve with different numbers of anti-cavitation trims,” Journal of Central South University, Vol. 25 No. 11, pp. 2677∼2687. [https://doi.org/10.1007/s11771-018-3945-y]
Van Doormaal, J. P., and Raithby, G. D., 1984, “Enhancements of the SIMPLE method for predicting incompressible fluid flows,” Numerical heat transfer, Vol. 7, No. 2, pp. 147∼163. [https://doi.org/10.1080/01495728408961817]

Working fluids	Flow parameters
-	Q/Q_ref	T/T_ref	σ
Water	0.5	3	2, 4
		5	2.5, 4
		7	2.5, 4
	0.8	3	0.9, 1.8, 2.7, 3.6
		5	2.5, 3.6
		7	2.5, 3.6
	1	3	0.5, 1, 1.5, 2, 2.5, 3.5, 5
		5	1, 2.5, 3.5
		7	1, 2.5, 3.5
Acetone	0.5	3	2
	0.8	3	1.8
	1	3	0.5, 1, 1.5, 2.5, 3.5
50/50 EGW	0.5	3	2
	0.8	3	1.8, 2.7
	1	3	0.5, 1, 1.5, 2.5

Thermophysical properties	Working fluids
Thermophysical properties	Water	Acetone	50/50 EGW
Liquid density [kg/m³]	995.61	779.02	1058.20
Liquid viscosity [kg/m s]	7.97×10^-4	2.92×10^-4	34.78×10^-4
Vapor density [kg/m³]	0.03042	0.90071	0.02393
Vapor viscosity [kg/m s]	9.86×10^-6	8.15×10^-6	8.22×10^-6