이차유로 누설 유동이 고압터빈 유동 및 효율에 미치는 영향

2.1 계산 영역 및 격자

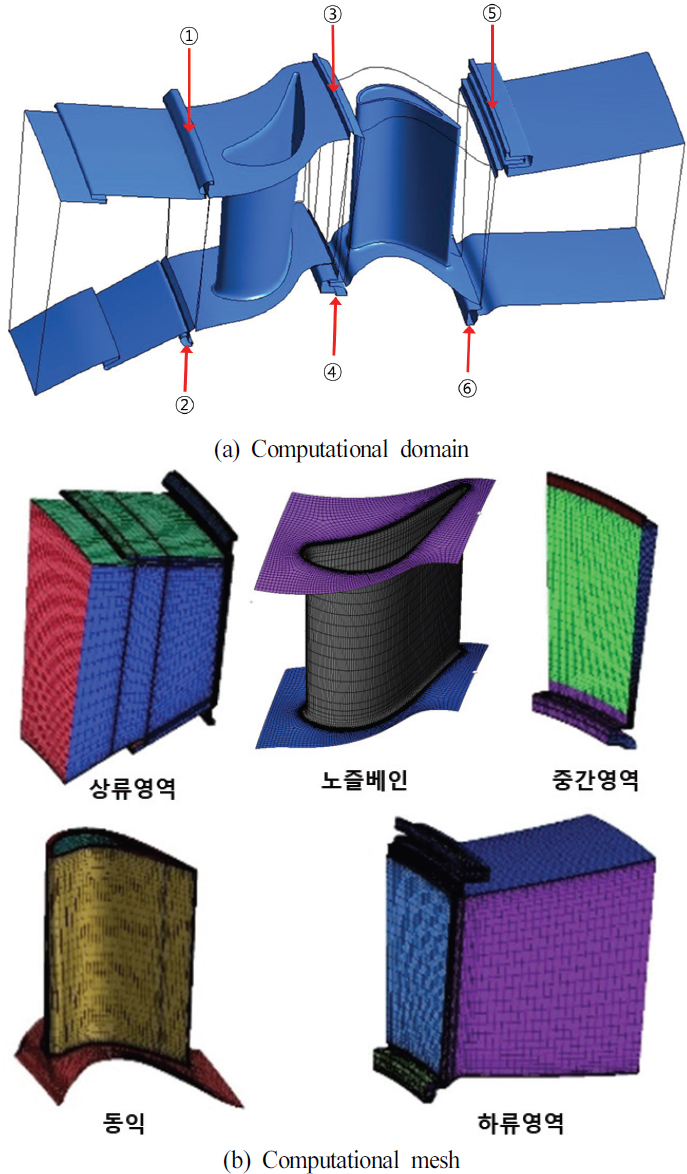
허브 및 슈라우드 누설 유동이 고압터빈 내부 유동과 공력 성능에 미치는 영향을 살펴보기 위해서, Fig. 1에 나타낸 것처럼 계산 영역을 국내에서 개발된 5,500lbf급 소형 가스터빈의 연소기 하류부터 고압터빈 하류까지의 영역으로 설정하였다. 일반적으로 터빈 유동해석에는 노즐베인과 동익의 상호작용이 중요하기 때문에 계산 영역을 노즐을 포함하는 유로와 동익을 포함하는 유로로 구성하였다. Fig. 1에서 ①∼⑥은 주유로로 유입되는 누설 유동의 이차유로 위치를 나타낸다. 이 연구에서는 허브와 슈라우드에 존재하는 6개의 누설유로를 모두 포함하기 때문에, 격자를 생성할 영역을 상류영역, 노즐 베인, 중간 영역, 동익 및 하류 영역의 5개로 분할하였다. 상류, 중간 및 하류 영역의 허브와 슈라우드에는 누설 유로가 배치되어 있다. 노즐 베인에는 허브 및 슈라우드 근처에서 필렛(Fillet)이 모두 구현되었고, 동익에서는 허브 필렛과 오목한 익단(Recessed tip)이 모두 구현되어 있다. 이렇게 분할함으로써 계산 영역 전체에 육면체 격자를 사용할 수 있으며, 각 유로에 사용되는 격자수를 손쉽게 설정할 수 있다. 각 분할된 영역에 사용된 격자수는 Table 1에 정리되어 있는데, 격자 의존성을 시험하기 위해서 총 격자수가 약 57만개, 120만개 및 235만개인 세 개의 격자를 생성하였다. 세 격자 모두 벽면에서의 y+값은 5∼10의 값을 사용하였다.

Fig. 1

Computational domain and mesh for high-pressure turbine

Table 1

Number of nodes for three different grids

2.2 계산 기법 및 경계 조건

고압터빈 내 3차원 정상상태 유동해석에는 상용 유동해석 프로그램인 Ansys CFX를 이용하였다. 질량 보존, 운동량 및 에너지 방정식의 대류항은 수치적인 확산에러를 최소화하기 위한 고-분해능(High-resolution) 기법을 사용하였고, 확산항은 FEM에서 사용되는 모양 함수(Shape function)을 이용하여 차분화되었다. 고압터빈 내의 유동은 난류로 가정하고 k-ω SST 모델을 이용하여 난류 점도를 계산하였다.

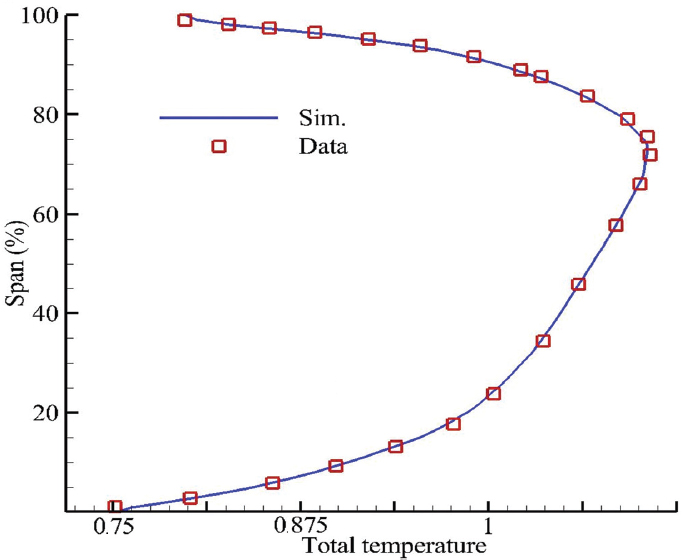
고압터빈 입구에서의 경계조건으로 연소기 하류 평균 전압력을 고정하였고, Fig. 2와 같이 스팬에 따른 전온도 분포를 적용하였다. 유동해석을 마친 후 계산 결과로부터 얻은 입구 전온도 분포는 고압터빈 설계에 사용된 분포와 잘 일치한다. 참고로 이 그림에서 전온도는 노즐 베인 입구 질량평균 전온도로 무차원하였다. 출구 경계조건은 터빈 하류 허브의 정압을 고정하고 반경방향 평형 방정식(Radial equilibrium equation)을 적용하여 각 스팬에서의 정압을 계산하여 사용하였다. 계산 영역간 인접면에서는 프로즌 로터(Frozen rotor)기법을 사용하여 유동 특성이 인접면에 전달되도록 하였다. 벽면에서는 노-슬립(No-slip) 조건을 사용하였고, 벽근처 첫 번째 격자점에서의 속도는 확장가능 벽함수(Scalable wall-function)를 사용하여 결정되었다. 노즐 베인과 동익은 각각 하나의 유로만 사용하므로 회전 주기 조건(Rotational periodic condition)을 적용하였다. 허브 및 슈라우드의 누설 유로에 대한 경계조건은 모두 설계 유량을 반영한 유량 조건으로 주었으며, 주유로 유량의 0.3∼0.7% 범위 내에 있다. 고압터빈 입구 가스 조건, 동익 코드 길이 및 익단 회전속도에 기반한 레이놀즈 수는 약 320만이다.

Fig. 2

Total temperature distribution just downstream of combustor on number of nodes

2.3 반응면 기법(Response surface method)

고압터빈은 복잡한 내부 유동, 주유동 및 여러 누설 유동 간의 상호작용 등으로 해석 결과가 선형관계가 성립되지 않기 때문에 제한된 비용과 짧은 시간 안에 관심 영역에서의 관계를 효과적으로 찾기 위해서는 대리 모델을 구축하여 분석하는 것이 필요하다. 이 연구에는 2차 다항식에 기반한 반응면 기법을 사용하였는데, 이 방법은 가능한 적은 수의 데이터를 이용하여 목적함수의 반응을 이끌어 내는 통계적인 분석 방법이다. 반응면 기법은 설계 변수를 2차 다항식으로 표현하며, 2차 다항식에는 교차항이 포함된다. 2차 회귀함수를 적용하기에 앞서 설계 변수를 식 (1)과 같이 선형변환해야 한다.

여기에서 ξ_i는 설계 변수이며 ξ_0i는 해당 설계변수 변화의 중심값이다. x_i는 선형변환된 새로운 설계 변수이며 C_i는 각 인자의 수준인데, 일반적으로 변수의 설계영역의 반으로 설정한다. 반응면은 새로운 설계 변수를 이용하여 식 (2)와 같은 2차 회귀모형 식을 통해 표현한다.

β는 회계분석에 쓰이는 미정 계수이고 n은 설계 인자의 수이다. 미정 계수와 새로운 설계변수를 이용하여 목적함수 Y를 표현한다. 미정계수는 최소자승법(Least square method)을 이용하여 구하며, 미정계수의 수는 전체 실험 횟수보다 작아야 한다.

3.1 누설 유동의 주유동에 대한 영향

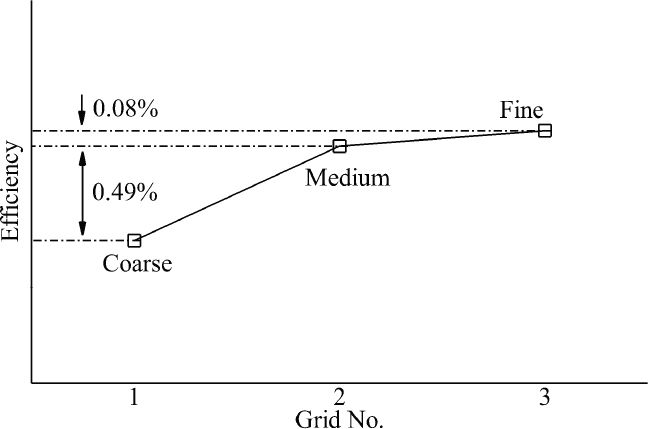
누설 유동이 주유동에 미치는 영향을 분석하기에 앞서, 수치해석 결과의 격자 의존성을 확인하였다. Table 1에 제시된 세 격자에 대해서 누설 유동이 있는 경우에 고압터빈의 효율을 계산하고, 결과를 Fig. 3에 비교하였다. 격자 1번(57만개)과 격자 2번(120만개)의 설계점 효율 차이는 0.49%이지만, 격자 2번과 격자 3번(235만개)의 효율 차이는 약 0.08%로 거의 차이가 없다. 더 많은 격자를 사용한다 하더라도 격자수에 따른 효율 차이는 작을 것으로 판단되므로, 격자 2번을 사용하여 누설 유량이 터빈 효율에 미치는 영향을 분석하였다.

Fig. 3

Efficiency variation depending

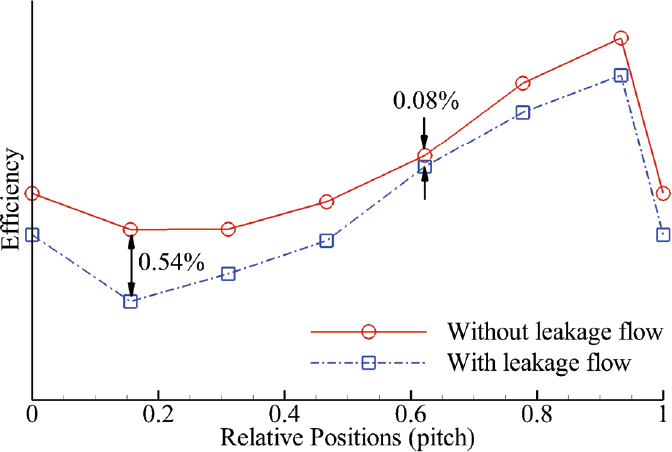
고압터빈의 노즐 베인과 동익 사이에 적용된 프로즌 로터 조건은 정상상태 해석에서 상류 익렬의 후류 효과를 고려할 수 있는 장점이 있지만, 노즐 베인과 동익의 상대적인 위치에 따라서 터빈의 성능이 변할 수 있다. 따라서, 노즐 베인과 동익의 상대적인 위치를 변화시키면서, 누설 유동이 있는 경우와 없는 경우에 효율 변화를 계산하고 Fig. 4에 나타내었다. 누설 유동이 없는 경우와 비교하여, 누설 유동이 있는 경우에는 노즐 베인과 동익의 상대위치에 관계없이 고압터빈 효율이 0.08∼0.54% 감소한다. 이 연구에서는 상대적인 피치 변화가 0인 경우를 사용하였으며, 이때 효율 감소는 0.31%로 상대위치 변화에 따른 효율 감소량의 중간 값이다.

Fig. 4

Efficiency variation depending on relative positions of rotor to nozzle vane

고압터빈 설계운전 조건에서 허브와 슈라우드의 누설 유동이 있는 경우와 없는 경우에 대해 유동해석을 수행하고 누설 유동이 설계점에서의 주유동에 미치는 영향을 먼저 분석하였다. 누설 유동을 제외한 다른 경계조건을 동일하게 유지하면서 계산한 결과, 누설 유동이 없는 경우에는 터빈 출구 유량이 설계값보다 0.01% 높게 예측되었고, 누설 유동이 있는 경우에는 유량이 설계값보다 약 2.5% 높게 계산되었다.

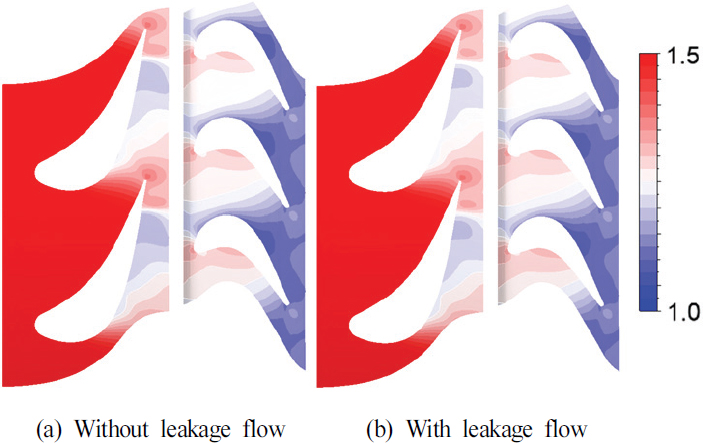
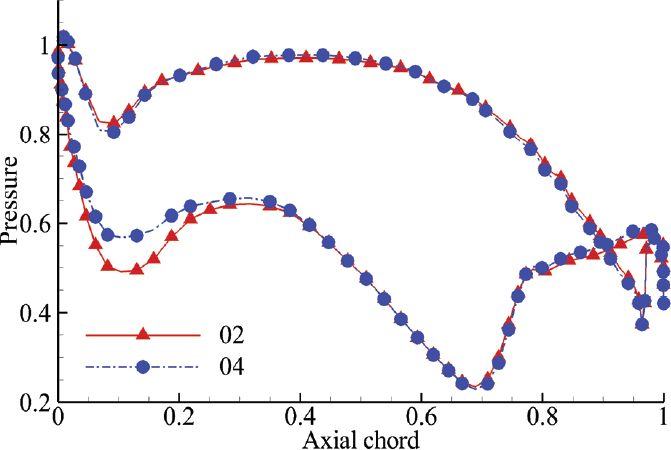
Fig. 5에는 누설 유동이 없는 경우와 있는 경우에 노즐 및 동익의 80% 스팬에서의 정압분포를 나타내었다. 압력은 누설 유동이 없는 경우의 동익 내 최저 압력으로 무차원하였다. 두 경우 모두 누설 유동의 유무에 관계없이 비슷한 유동현상을 나타내고 있다. 노즐 흡입면 압력분포에서 차이가 발생하지만, 동익 내의 유동은 거의 동일하다. 고압터빈 설계 운전점에서 누설 유동이 허브 및 슈라우드 근처의 유동에는 큰 영향을 미칠 수 있지만, 20%∼80% 스팬에 걸쳐 있는 코어 유동에는 영향력이 제한적임을 알 수 있다. 참고로, 마하수 분포와 유선을 확인해도 코어 유동은 누설 유동의 유무에 관계없이 거의 일정하다.

Fig. 5

Static pressure distribution at 80% span

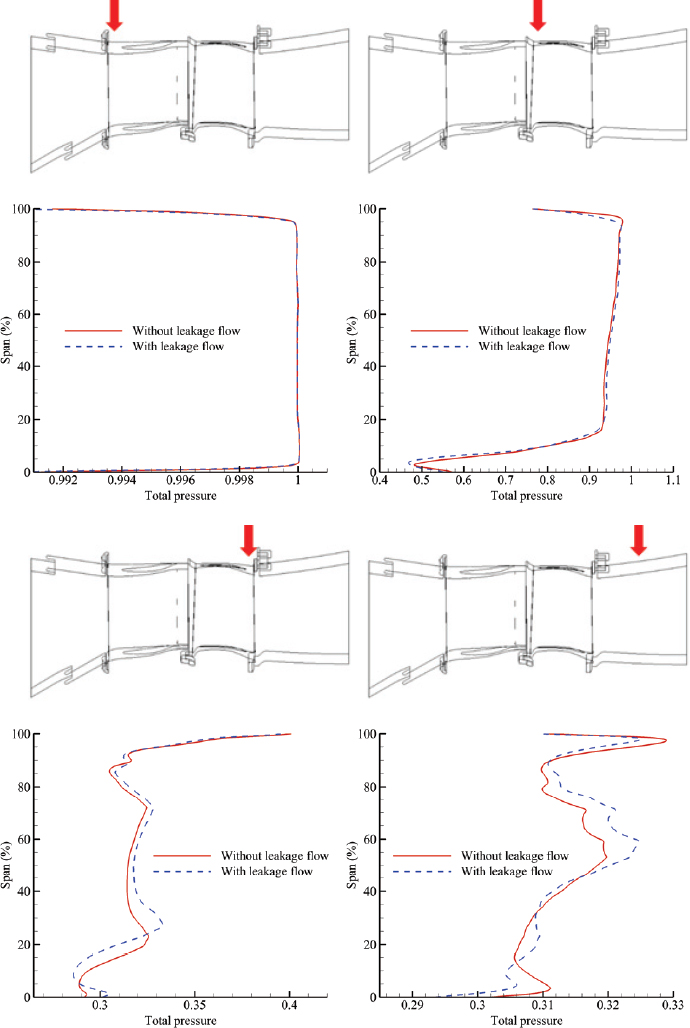
Fig. 6은 누설 유동이 없는 경우와 있는 경우에 고압터빈 내부 네 위치에서 스팬에 따른 전압분포를 나타내었다. 전압은 노즐 베인 입구 평균 전압으로 무차원하였다. Fig. 1에 나타난 것처럼, 노즐 상류의 유동은 누설유동 ① 및 ②의 영향을 받고, 동익 상류 및 하류의 유동은 누설 유동 ①∼④의 영향을 받으며 터빈 하류의 유동은 6개 누설 유동의 영향을 받는다. 노즐 상류의 그림에서는 누설 유동의 유무에 관계 없이 동일한 전압 분포가 나타나는데, 이것은 누설유동 ① 및 ②가 주유동에 미치는 영향이 제한적임을 의미한다. 동익 상류에서는 허브 및 슈라우드 근처에서 누설 유동에 의해서 전압이 상당히 감소하지만, 20∼80% 스팬에서의 유동은 일정함을 확인할 수 있다. 동익 하류 및 터빈 하류에서는 누설 유동에 의한 영향이 스팬방향으로 전파되면서 허브 및 슈라우드에서는 전압이 낮게 나타나지만, 코어 유동에서는 전압이 높아지게 된다.

Fig. 6

Spanwise total pressure distribution at each streamwise position

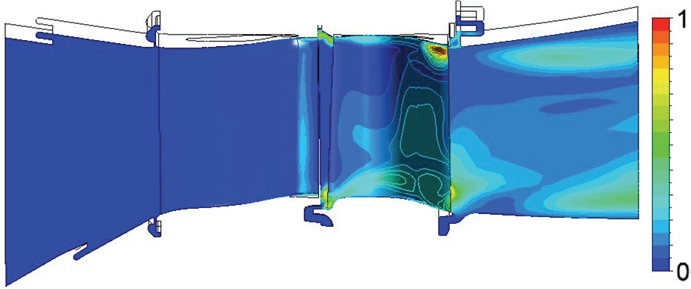
허브와 슈라우드에서 발생하는 누설 유동이 터빈 내부 주유동에 미치는 영향을 살펴보기 위해서, 각 계산영역의 주기면(Periodic surfaces)에서의 난류 운동에너지 분포를 Fig. 7에 나타내었다. 난류 운동에너지는 터빈 주기면 내 최대값으로 무차원하였다. 전압분포에서 확인한 것처럼 누설 유동 ① 및 ②는 노즐 상류 주유동과 혼합되지 않고 허브와 슈라우드에 부착되어 하류로 이동한다. 반면에 누설 유동 ③ 및 ④는 동익 유로에서 주유동과 혼합되면서 높은 난류 운동에너지를 나타낸다. 특히, 허브에서 유입되는 누설 유동은 동익 유로에서 20% 스팬까지는 영향을 미치는 것으로 판단할 수 있다. 동익 하류의 누설 유동 ⑤ 및 ⑥은 주유동과의 혼합에 의한 난류 운동 에너지 증가는 크지 않은 것으로 확인되는데, 이것은 동익에서 주유동 에너지의 상당부분이 동력으로 전환되고 유체 압력 및 속도가 감소하여 누설 유동과의 상호작용이 줄어들기 때문이다. 그러나, 터빈 하류 영역에서 출구에 가까워질수록 허브와 슈라우드 근처에서 난류 운동에너지가 높은 영역이 나타나는데, 이 혼합영역은 노즐 및 동익의 후류(Wake)가 지나는 영역으로 판단된다.

Fig. 7

Turbulence kinetic energy distribution on periodic surfaces with leakage flows

3.2 누설 유동의 효율에 대한 영향

누설 유동 ① 및 ②는 터빈 내부 유동에 미치는 영향이 제한적이므로, 누설 유동의 유량 변화에 따른 주유동 손실의 변화를 파악하기 위해서 누설 유동 ③∼⑥의 유량을 변화시키면서 누설 유동이 없는 경우와 비교하여 효율 감소(△η) 및 동익 1개의 토크 감소(△τ)를 Table 2에 정리하였다. 각각의 누설 유동에서 유량 변화는 ±50%로 제한하였으며, Box-Behnken의 방법에 따라 실험계획법에서 해석할 25개의 경우를 결정하였다. Box-Behnken 방법은 반응면 기법을 적용하기 위한 실험계획 시 전배치법(Full-factorial design) 대비 실험 횟수를 줄이면서도 2차 모델의 적합성을 극대화 할 수 있는 방법이다 [11]. 고압터빈에서 누설 유량이 없는 경우에 비해서 설계 누설 유량을 가지는 경우 약 0.309%의 효율 감소와 0.4692N⋅m의 동익 토크 감소가 있는 것으로 예측되었고, 특히 누설 유동 ③ 및 ④의 유량이 동시에 50%씩 증가된 경우에는 효율은 0.501%, 토크는 0.6781N⋅m 감소하였다.

Table 2

DOE generated by Box-Behnken method

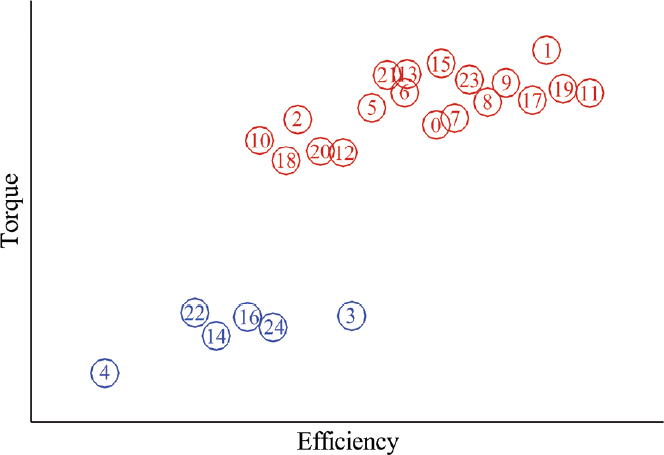
효율과 터빈 동익에 작용하는 토크의 관계를 확인하기 위해서 Table 2의 25개 경우에 대해서 두 변수의 상관관계를 Fig. 8에 나타내었다. 일반적으로 터빈의 경우 효율이 증가할수록 동익의 토크가 증가하는 양의 상관관계를 가지게 되는데, 이 연구에서도 동일한 결과를 확인할 수 있다. 그러나, 누설유동 ④의 유량이 증가되는 경우(3, 4, 14, 16, 22, 24)에는 토크가 급격히 감소하는 현상이 나타난다. Fig. 9에는 Table 2의 2번 및 4번 경우에 대해서 동익 10% 스팬에서 동익 전연에서의 압력으로 무차원화 된 압력분포를 나타내었다. 누설유동 ④가 증가함에 따라 허브 근처에서 유동의 입사각이 감소하여 동익의 부하가 크게 감소함을 확인할 수 있다. 이 때문에 다른 누설 유동에 비해서 상대적으로 누설유량이 큰 누설 유동 ④의 유량이 증가하면 토크의 급격한 감소가 나타나게 된다.

Fig. 8

Relationship between efficiency and torque

Fig. 9

Blade loading at 10% span

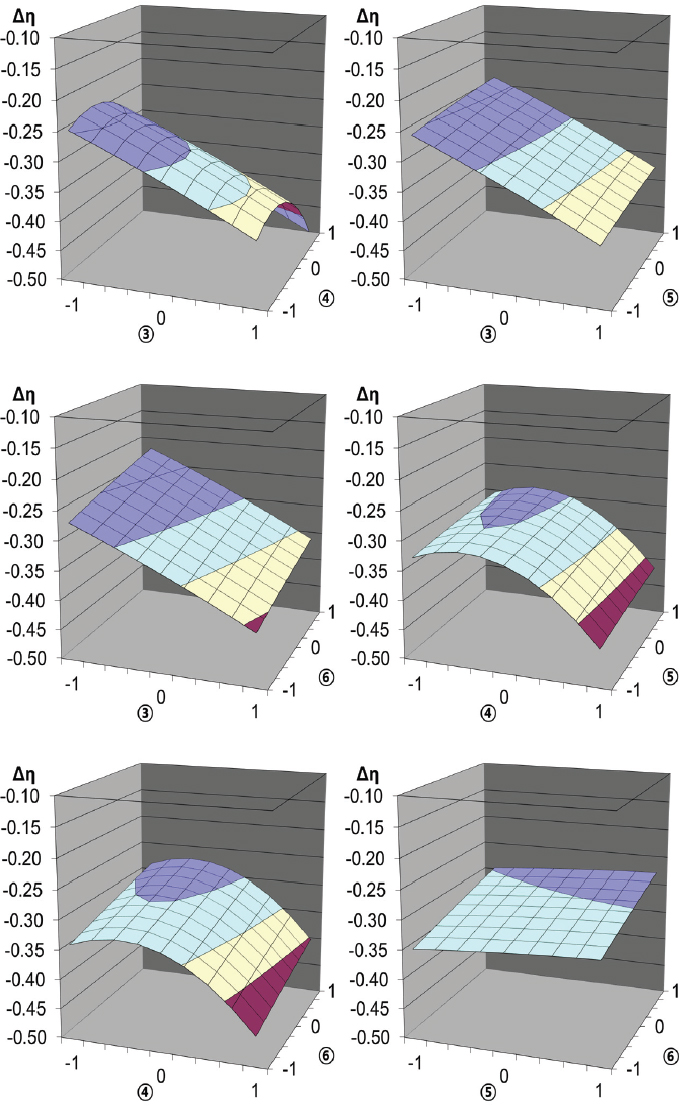
각 누설 유동이 고압터빈 효율에 미치는 영향을 분석하기 위해서, Table 2의 결과를 이용하여 식 (2)의 2차 회귀함수를 구하였고 각각의 누설 유동에 대한 반응면을 그려 Fig. 10에 나타내었다. 여기에서 설계 변수는 누설 유동 ③∼⑥의 유량이며 목적함수는 Table 2에 정리된 효율 감소이다. 총 6개의 반응면을 분석하면, 각 누설 유동이 고압터빈 효율에 미치는 영향을 아래와 같이 세 가지 내용으로 정리할 수 있다. 첫 번째, 동익 하류에 위치하는 누설 유동 ⑤와 ⑥은 노즐과 동익 사이에 위치하는 누설 유동 ③과 ④에 비해서 고압터빈 효율 감소에 미치는 영향이 적다. 두 번째, 노즐과 동익 사이 슈라우드에 위치하는 누설 유동 ③은 유량이 증가할수록 효율이 감소하는데, 이러한 결과는 서론에서 소개한 다른 연구자의 결과와도 일치한다. 세 번째, 노즐과 동익 사이 허브에 위치하는 누설 유동 ④는 유량이 설계값일 때 효율 감소가 가장 적고 유량이 감소하거나 커지면 효율 감소가 증가한다.

Fig. 10

Efficiency reduction depending on each leakage flow

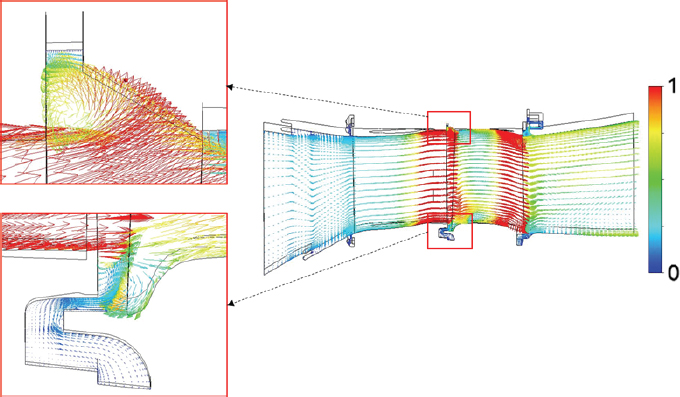
누설 유동 ④의 유량이 고압터빈 효율에 미치는 영향을 분석하기 위해서 Fig. 11에는 주기면에서의 속도 벡터를 나타내었다. 이 그림에서 속도 크기는 주기면 내 최대값으로 무차원하였다. 누설 유동 ④는 6개의 누설 유동 총 유량의 약 1/3을 차지하며, 다른 누설 유동과 달리 노즐과 동익 사이에서 상대적인 움직임을 가지는 휠스페이스에서 넓은 출구를 통해 주유동으로 흘러간다. Fig. 11의 하단에 나타난 누설 유동 ④를 살펴보면, 설계 유량보다 유량이 큰 경우에는 누설 유동과 주유동의 혼합이 많이 발생하여 손실이 발생하고, 설계 유량보다 유량이 적은 경우에는 주유동이 누설 유로로 일부 유입되어 손실이 증가하는 것으로 판단된다.

Fig. 11

Velocity vector on periodic surfaces with leakage flows