고성능 1MW급 펌프 수차 시스템 개발
Abstract
As variable renewable energy (VRE) has experienced rapid growth in recent years, its intermittent nature creates a significant demand for effective energy storage solutions. There has been increasing interest in small- and medium-sized pumped-storage hydropower stations with capacities under 100 MW. These systems are more environmentally friendly and are generally more accepted by communities compared to traditional large-scale projects. This makes them both practical and cost-effective options for storing variable energy.
This study focuses on developing an innovative design for a high-performance 1 MW-class pump-turbine system. This system represents a significant initial step toward localizing the primary components of pumped-storage hydropower systems in Korea. The design process utilizes a direct optimization technique based on a three-dimensional inverse design method and a multi-objective genetic algorithm. The new system was optimized to enhance efficiency and mitigate cavitation, one of the major undesirable phenomena in turbomachinery. The stability of the pump-turbine system structure was ensured through finite element method (FEM) analysis, enabling it to withstand the severe operating conditions of the system.
Compared to the performance results of the baseline model (Design 1) based on three-dimensional inverse design method, the newly developed pump-turbine system (Design 2) has significantly expanded its operational range in both turbine and pump modes due to enhanced cavitation performance during partial and overload conditions. The newly developed 1 MW-class pump-turbine system achieved over 80% efficiency even at partial loads exceeding 60%, with a maximum efficiency of 91.2% in pump mode and 90.5% in turbine mode. Notably, energy savings are realized through reduced power consumption, thanks to the remarkable performance improvements in pump mode.
Keywords:
Pumped-storage hydropower system, Pump-turbine system, Inverse design method, Optimization algorithm, CFD키워드:
양수 발전시스템, 펌프 수차 시스템, 역해법 설계법, 최적화 알고리즘, 전산 유체 역학1. 서 론
온실가스 감축과 탄소 중립의 적기 이행 목적으로 신재생에너지 보급이 급속도로 진행되고 있다. 신재생에너지 발전 설비 중에서도 변동성 전원 즉 출력 변동, 간헐성 출력을 기본 특성으로 하는 가변재생에너지(variable renewable energy: VRE)인 태양광과 풍력발전의 보급이 확산하고 있다. 또한, 우리나라는 전력 소비지역과 대규모 발전소로 전력공급 지역이 지리적으로 떨어져 있어 지역 편중을 극복하기 위해 장거리 송전설비를 이용해야 하는 구조이다. 재생에너지 증가와 함께 수반되는 발전 수요간 지역 편중 심화 현상과 최근 AI에 관련된 산업 구조 개편으로 전력수요의 증가에 대응하기 위해서는 신규 대형 송전선로 신설과 유연성 자원의 보충이 필수적이다. 신규 송전선로 건설은 주민 수용성 등 사회문제가 야기되고 있다. 유연성 자원으로서 대규모 양수 발전소 건설도 주민 수용성, 환경 문제, 건설 기간, 적정 장소의 한정 등의 문제점을 가지고 있다.
따라서 신재생에너지의 변동성에 대한 전력 계통의 안정성을 유지하기 위한 대안으로 가장 경제적이고 신뢰성 있는 유연성 에너지원으로서 소규모(100 MW 이하) 양수 발전이 장주기 에너지 저장 장치로서 차세대 스마트 그리드 구축을 위한 핵심 기술의 하나로 부각하고 있다.
국내에는 원자력이나 화력 등 기저발전의 보조용으로 대형 양수 발전소가 전국에 7곳이 산재해 있다. 양수 발전소의 핵심인 주기기인 펌프 수차와 발전 전동기는 전부 외산인 실정이다. 따라서 2023년에 정부와 한수원의 지원으로 소형 양수발전을 위한 주기기 기술 국산화 과제가 시작되었다.(1,2)
본 연구는 100 MW 이하 소형 양수발전용 주기기인 개발의 출발점으로 고성능 1 MW급 펌프 터빈 시스템을 1차원 유선 해석법(Meanline analysis), 3차원 역해법(Three dimensional inverse design method), 실험 계획법(Design of Experiment: DoE), 반응 표면 법(Response surface method: RSM), 그리고 유전자 알고리즘을 이용한 다목적 최적 설계법(Multi-objective genetic algorithm: MOGA)으로 개발하였다.
이 시스템의 특징은 펌프 수차를 통해서 펌프 모드 와 터빈 모드를 계속 반복하기 때문에 펌프의 성능과 터빈의 성능이 상충하는 부분에서는 시스템의 안정성을 우선하여 절충(trade-off)하였다.
2. 펌프 터빈 시스템 설계
1 MW급 펌프 수차의 수력학적 사양은 Table 1과 같다.
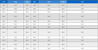
펌프 수차 설계의 출발점으로 먼저 펌프 수차의 특성을 규명해볼 필요가 있다. Table 1의 데이터를 바탕으로 예비설계 단계로서 펌프시스템의 성능을 유추해 볼 수 있는 NsDs 터빈 차트에 Balje Cordial line과 펌프의 하한 유량과 상한 유량, 그리고 터빈 모드의 설계 포인트를 Fig. 1에 나타내었다. 선도에서의 비속도(specific speed)와 비직경(specific diameter)은 아래와 같이 정의하였다.(3)
| (1) |
| (2) |
| (3) |
| (4) |
여기서 N : 펌프 수차 회전수, Q : 유량, H : 수두(양정),
D : 펌프 수차 러너 직경, Cm: meridional velocity,
Cθ : tangential velocity, U : local rotational speed
이 선도를 보면 큰 틀에서의 펌프 수차의 형태 등 이상적인 설계 방향을 유추할 수 있어 개념단계에서 펌프 수차의 형식 및 크기와 개략적인 특성을 판단할 수 있는 유용한 자료이다. Fig. 1에서 알 수 있듯이 본 펌프 수차 시스템 기본 설계에 선정된 펌프 수차 직경, 유량, 양정, 그리고 회전수를 기반으로 상기 식에서 계산된 Ds와 Ns를 아래 Fig. 1에 도식하면, 세 개의 점(터빈 최적 설계, 펌프 최소 유량 그리고 최대 유량) 모두 이상적인 Balje의 cordial line 선상에 배치되어 Blade loading과 Flow coefficient가 적정히 배분되는 최적 설계 조건상에 배치되고 있음을 알 수 있다.
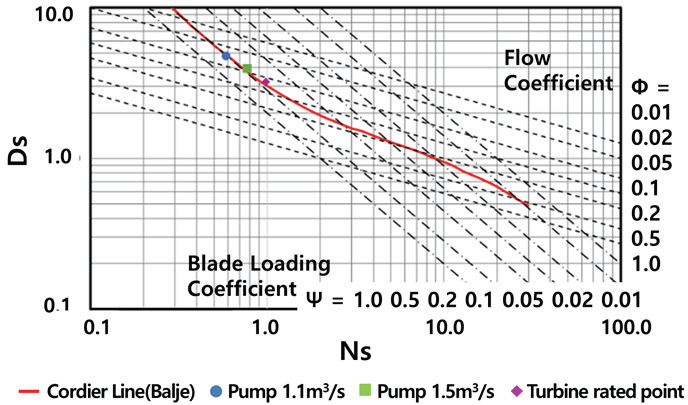
1 MW급 펌프 터빈 시스템 설계는 펌프 수차의 수력학적 요구 성능(펌프 모드 와 발전 모드)에 대하여 동시에 적정한 성능을 만족하도록 설계해야 하므로 종래의 펌프 설계나 수차 설계 방식을 적용하기 어려운 점이 있다. Fig. 2에 전체 설계 프로세스를 나타내었다.
우선 1차원 평균 유선 법으로 시스템에 대한 기본적인 파라미터 값과 자오면 형상을 바탕으로 펌프 모드와 터빈 모드에 대한 자오면 형상을 결정한 후 자오면 파라미터(8개)와 블레이드 로딩분포 파라미터(8개)와 블레이드 경사각(lean angle) 파라미터 1, 총 17개의 파라미터에 대해 3차원 역해법 설계법으로 블레이드의 3차원 형상을 설계한다.
스테이 베인과 가이드 베인은, 러너 형상 설계와 동일한 순서로 설계를 진행한 후 이에 매칭 되도록 스파이럴 케이싱과 흡출관을 설계한다. 수력학적 목표 성능은 수치 해석을 통해 확인하였다. 만족 여부에 따라 최적 설계를 할지 종료할지를 선택한다. 최적 설계는 스파이럴 케이싱을 제외한 러너 블레이드를 중심으로 다목적 최적화 기법과 역설계 형상 솔버(solver)로 직접 최적화한 후 가이드 베인 과 스테이 베인, 그리고 흡출관에 대해서 매칭이 되도록 시스템 재설계하였다.
2.1 펌프 수차 meanline analysis 및 자오면 설계
펌프 수차의 자오면 형상을 확정하기 위하여 우선으로 펌프와 수차와의 운전특성 차이를 확인하여야 한다. 펌프와 수차 운전조건으로 각각 meanline 설계를 실시한다.
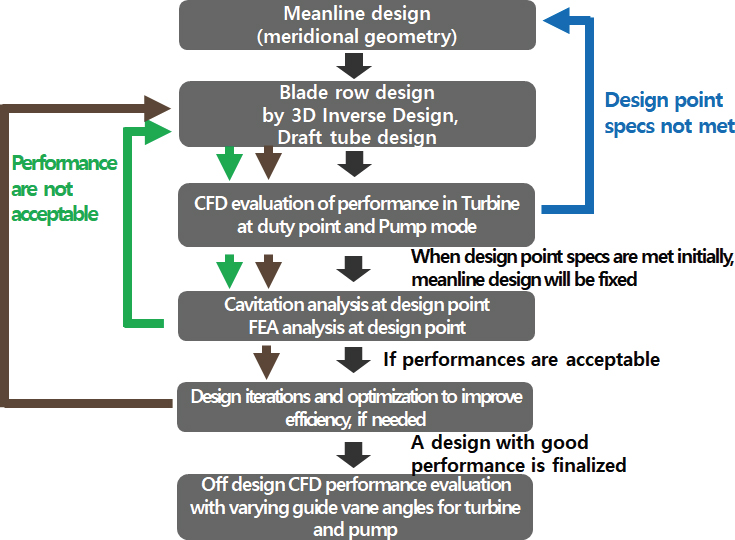
펌프 수차의 meanline 해석 결과를 Fig. 3에 도시하였다.
우선 펌프 대한 meanline 설계에서는 전술한 바와 같이 저 유량 조건과 고 유량 조건으로 나누어지는데, 이들 각각에 대하여 meanline 설계를 진행하면 아래 Fig. 3처럼 터빈 모드(정격), 펌프 모드의 유량 하한과 상한일 때의 효율, 블레이드 입구 및 출구직경, 스파이럴 케이싱(Spiral casing: SC) 입구 직경 값들과 기본 형상이 정해진다. 터빈 모드일 때의 블레이드 개수는 11개, 펌프 모드일 때는 6개로 각각 상이 하다.
펌프 수차의 러너 블레이드, 스테이 베인, 가이드 베인, 스파이럴 케이싱, 그리고 흡출관의 기본 치수를 최적화하기 위한 Meanline설계는 상용프로그램인 Turbodesign suite Pre를 사용하였다.(4)
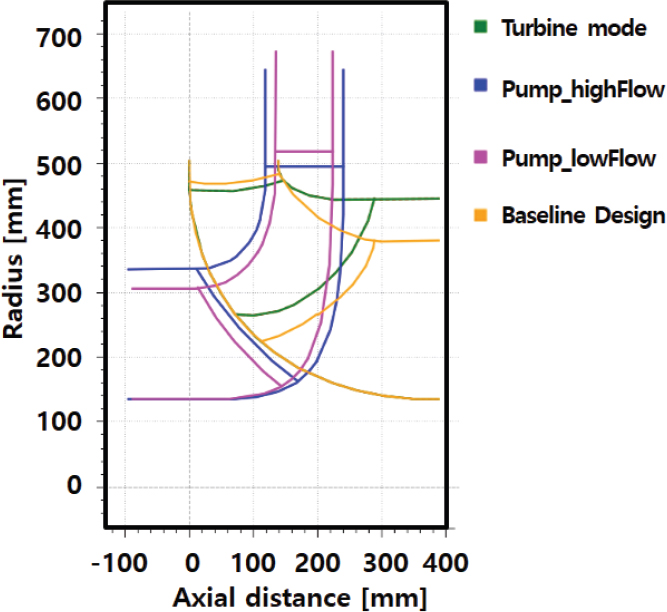
Meanline design에 의한 펌프 및 발전 모드의 meridional geometry를 Fig. 4에 비교하였다. 도시된 바와 같이 펌프모드, 발전 모드 다른 유량과 수두로 shroud와 Tip 직경이 다른 것을 확인할 수 있다.
펌프수차의 최고 성능을 위한 자오면 형상 설계 시 최상의 trade-off 값을 찾기 위해 몇 번의 계산이 필요하다.
펌프 모드에서는 meanline sizing에서 제시한 블레이드 개수 6개보다 증가하면 profile loss가 증가하고 효율이 떨어진다. 반면에, 터빈 모드에서는 블레이드 개수 변화에 효율 변화가 미미하다. 블레이드 개수는 시스템 효율성 및 제작 용이성을 고려해야 한다. 따라서 펌프 수차의 블레이드 개수는 6개와 11개의 trade-off로 최종적으로 8개가 최적 선택 되었다.
펌프 수차의 배이스라인 자오면 형상은 터빈 모드 geometry와 두개의 펌프모드 geometry에 대해서 meanline analysis에 의해 Fig.4와 같이 최종적으로 결정되었다.
스테이 베인과 가이드 베인의 블레이드 개수는 터빈 모드만 고려하여 선정하였다. 본 연구에 사용된 meanline analysis 상용 소프트웨어(TURBOdesign Suite)는 펌프 모드 형상 러너 블레이드이외의 하류의 가이드 베인, 스테이 베인 최적 구성을 지원하지 않고, 통상 펌프수차 설계 시 가이드 베인, 스테이 베인 구성은 터빈(발전) 모드를 기준으로 정한다. 따라서, 펌프 모드 시 러너 하류의 가이드 베인 과 스테이 베인의 개수는 터빈 모드의 meanline sizing를 바탕으로 블레이드 개수를 21개로 채택하였다.
터빈 모드 및 펌프 모드 별 meanline analysis 값은 Table 2와 같다.
2.2 3차원 역해법 설계(3-dimensional inverse design method)
터보 기계의 3차원 형상 설계는 런던대학의 Zangeneh에 의해서 제안된 설계 방법이다(4,5). 이 방법의 핵심개념은 유체역학적 지배 방정식에서 역으로 형상을 도출한다는 것이다.
회전하는 터보 기계의 러너 블레이드 사이의 흐름을 비압축성, 비점성, 비 회전 포텐셜 흐름(potential flow)이라는 가정하에 수차 러너와 유체와의 에너지 교환량은 다음의 오일러(Euler)식으로 표현할 수 있다.
| (5) |
식(5)을 단위 질량 당 각운동량 변화로 표현하면 다음과 같다.
| (6) |
여기서, g: 중력 가속도(m2/s), H: 수두(m), η: 효율, w: 각속도(rad/s).
즉, 유체의 단위 질량 당 각운동량 변화로서 주어진 러너 블레이드의 순환(Γ=2πrCu)분포를 규정한다는 것을 알 수 있다.
원주 방향의 속도 성분(Cu)으로 인하여 쿠타-쥬코스키(Kutta–Joukowski) 이론에 따라 블레이드에 속박 순환(bound circulation)이 발생하고 속박 와(vorticity)의 와면 강도(vortex sheet intensity)를 박익(thin airfoil) 이론에 따라 블레이드의 캠버 선(camber line)으로 설정하고 캠버 선(camber line)에 따른 두께 분포를 Naca profile을 통해 블레이드의 기본 형상을 설계한다.
이처럼 역해법 설계법은 종래의 직접 설계처럼 블레이드 형상을 형상 파라미터 변환에 의한 시행착오와 설계자의 경험에 의존하지 않고, 포텐셜 흐름이라는 이상적인 흐름장의 조건에 맞는 러너 블레이드 형상을 역으로 컴퓨터로 실현하는 설계 방법이다.
펌프 수차 러너 사이의 흐름은 포텐셜 이론에 근거하여 점성의 영향은 무시하였지만, 흐름의 박리(separation)가 없는 한 정압분포에 관해서는 점성의 영향이 크게 좌우되지 않기 때문에 블레이드 상하면에 작용하는 압력분포는 다음과 같이 표현된다.
| (7) |
여기에서 : 블레이드 압력 면의 정압, : 블레이드 흡입 면의 정압, Z : 블레이드 개수, ρ : 작동 유체의 밀도, : 평균 자오면 절대속도, m : 자오면 방향, : 원주 방향 평균 속도, : swirl 속도.
식 (7)에서처럼 블레이드 압력 면과 흡입 면의 정압 차이는 역 해법의 설계 파라미터인 원주 방향 평균 각운동량()의 자오면 방향 변화량(∂()/∂m)에 의해서 제어할 수가 있다는 것을 알 수 있다. 이처럼 블레이드 부하분포(자오면 방향 부하분포와 입구와 출구에서의 스펜 방향 부하분포)는 역해법 설계에 가장 중요한 변수 중의 하나이다.
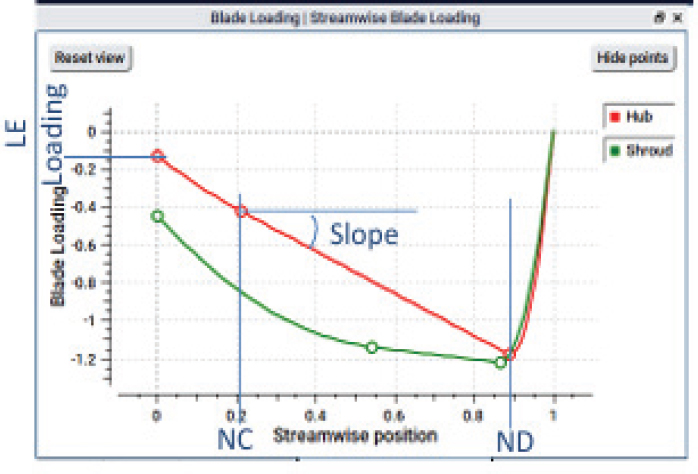
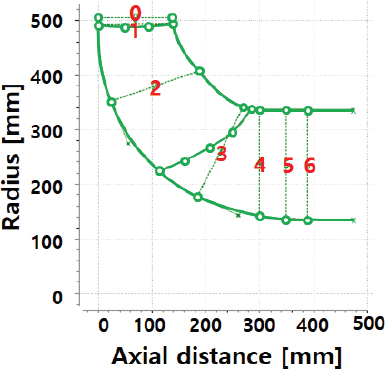
Fig. 5에 펌프 수차 러너 블레이드 설계에 사용된 로딩 부하분포를 나타내었다.
블레이드 부하분포는 포물선, 직선, 그리고 포물선 3개의 영역으로 나누고 블레이드 전연(leading edge, m=0)에서 입사각으로 인한 부하분포의 미분 값은 Incidence라는 파라미터로 나타내고 후연(trailing edge,m=1)에서는 쿠타(Kutta) 조건에 의해서 값은 항상 0이다. 쉬라우드(shroud)와 허브(hub) 직경 등 자오면에 총 7개의 설계 파라미터, 로딩 분포(Incidence, NC, ND 그리고 slope)에 8개 파라미터, 마지막으로 블레이드 비틀림 각도(lean angle) 1개로 총 17개의 파라미터 입력으로 아주 짧은 시간에 블레이드의 형상을 컴퓨터로 설계한다.
2.3 베이스라인 디자인(Design 1)
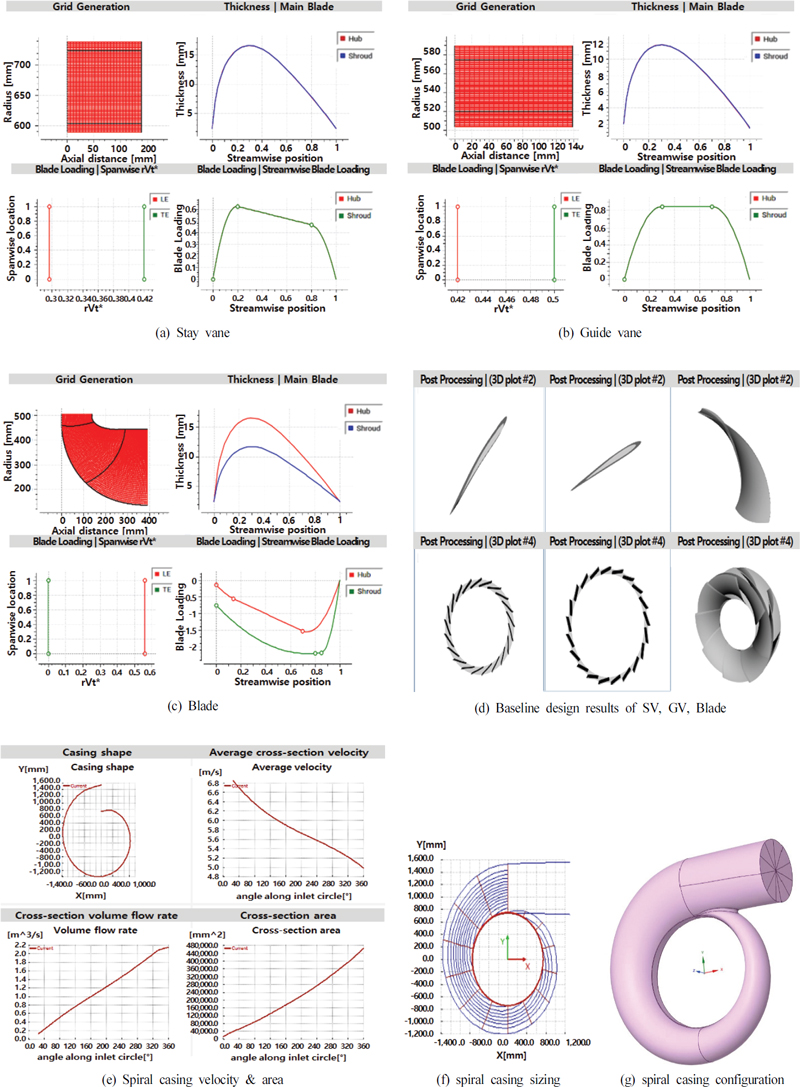
Meanline analysis에 근거하여 역해법 기법에 따라 스테이 베인, 가이드 베인, 러너 블레이드, 스파이럴 케이싱 형상을 Fig. 6에 나타내었다.
자오면 형상, 블레이드 로딩분포와 NACA Profile을 입력값으로 ADT사의 상용프로그램인 Turbodesign suite TD1을 사용하여 Fig. 6a∼Fig. 6f처럼 설계하였다.(4)
스파이럴 케이싱 과 흡출관 설계는 블레이드 열 설계 과정과는 다른 방법으로 접근하기 때문에 별도 설명한다.
스파이럴 케이싱은 펜스탁(penstock) 과 스테이 베인 사이에 물을 균일하게 흐르게 하여 러너가 최상의 성능을 발휘하도록 유도하는 통로이다. 설계 시는 터빈 모드에서 질량 보존과 각운동량 보존 법칙에(Cu.R=Γ=constant) 따라 meanline 해석에서 얻은 모든 치수 들과 케이싱 출구에서의 반경 방향 속도(3.41m/s)와 접선 방향 속도(6.43m/s)를 전 각도에 대한 경계조건(일정)으로 역해법에 근거하여 2차원 유선법(stream curvature method)을 사용하여 원주 방향 면적분포는 각 단면에서의 크기를 수치적 반복 계산으로 형상을 설계한다.
베인 입구 vortex와 스파이럴 케이싱의 계산된 vortex 값이 일치할 때까지 반복을 수행한다. 최종적으로 형상과 성능을 검증한다.
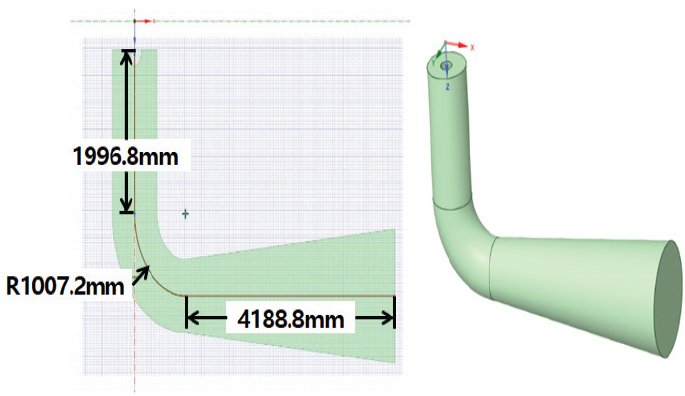
흡출관(draft tube)은 압력 맥동을 최소화하고, 부분 부하 조건에도 재순환영역에 의한 에너지 손실을 최소화하기 위하여 자체 설계 툴을 사용하여 Fig. 7처럼 설계하였다.
흡출관 출구 부에서 유속이 충분히 낮아져서 확산 손실을 최소화하기 위하여 확산 각을 5.10로 하고, 확산 길이는 약 4.6m로 설계하였다.
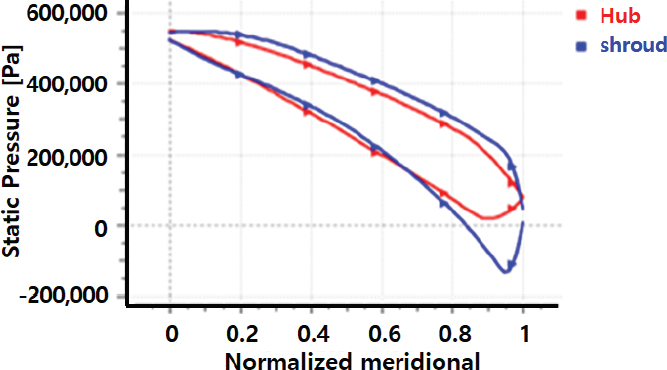
기본 설계1의 블레이드 표면의 압력분포를 Fig. 8에 나타내었다. 허브(hub)의 압력분포는 전연(leading edge)이나 후연(trailing edge) 어디에서도 음압이 발생 되지 않지만 쉬라우드(shroud)의 후연 부분에서 음압이 발생하고 있다는 것을 볼 수 있다. 이것은 캐비테이션이 발생할 수도 있다는 의심을 가지게 된다.
1차원 meanline analysis와 3차원 역해법 결과를 바탕으로 얻은 3차원 펌프 수차 시스템 형상에 대해 성능 스피드 라인(speedline) 해석을 한 결과는 Table 3과 같다.
Table 3에서 알 수 있듯이 펌프 모드의 수치 해석 결과, 시스템 목표 효율(정격조건 수차 모드: 87%, 펌프 모드: 88%)에 미흡하다는 것을 알 수 있다.
기본 러너 블레이드 형상으론 수차 모드에서는 어느 정도 목표치를 달성하였지만, 펌프 모드시 유체가 펌프 러너를 통과할 때 블레이드 면에 유체의 불안정성이 발생하여 전체 시스템 효율을 저하하고 있다는 것을 알 수 있다.
펌프 모드의 성능향상과 터빈 모드의 안정화를 위해 다목적(Multi-Objective) 유전자 알고리즘을 이용한 최적화를 실시하였다.
2.4 최적 설계
다목적 최적화(MOGA)는 결국 전체 solution 중에 파레토(Pareto) 최적인 solution 집합을 찾는 문제이다.(6)
본 영구에 사용된 러너 형상 최적화의 입력 파라미터와 변위 범위에 대한 것을 Table 4에 나타내었다.
Table 4에서처럼 자오면 stream 방향 로딩 분포(파라미터 8개), 자오면 파라미터 8개, 그리고 블레이드 wrap 각도, 총 17개의 입력 파라미터를 형상 solver인 TD1에 입력하여 형상을 구하고, 파라미터들을 이용하여 MOGA를 통해 최적해를 구한다. Fig. 9에는 Table 4에서의 자오면 매개변수들을 적용할 자오면을 도시하였다.
Fig. 9에서처럼 자오면 파라미터는 Table 4의 input parameter 중 9번부터 16번까지 파라미터의 변위 하한과 상한 범위 내에서 조정된다.
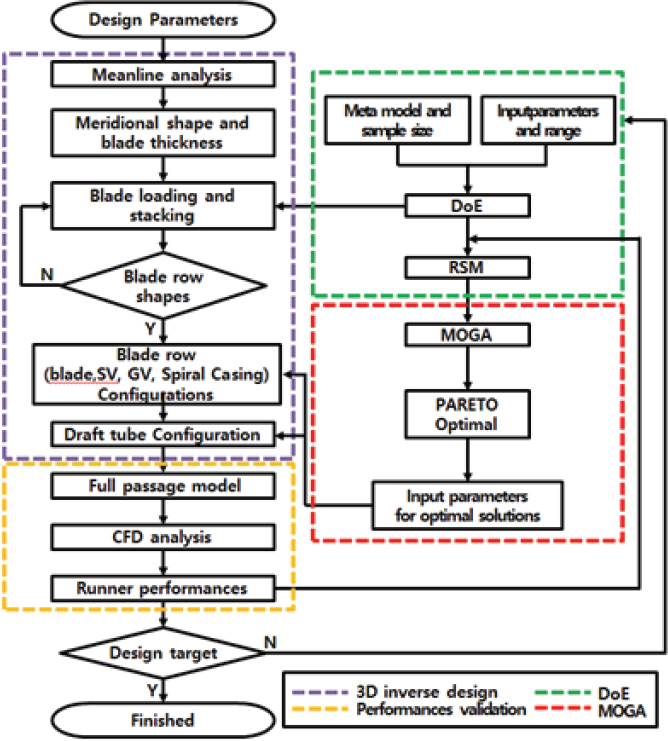
Fig. 10에 기존에 많이 사용되던 펌프 수차 DOE와 SRM대체 모델을 이용하는 최적화 방법의 흐름도를 도시하였다.
대체모델(surrogate model) 기반 최적화 법은 파라미터 수를 줄이기 위한 수단으로 샘플링(sampling) 기법을 사용하여 DoE(실험 계획) 행렬을 생성한다. 이 행렬은 선택된 입력 매개변수의 양에 따라 약 100-150개의 설계 정도로 축약된 설계를 가질 수 있다. 따라서 CFD와 결합할 수 있는 정도지만 검증해야 할 sample수가 아직 많다. 샘플링기법은 민감도 분석(sensitivity analysis)을 통해서 많은 파라미터 중에서 가장 영향력 있는 파라미터를 도출하는 원리지만, 전술한 바와 같이 아직도 검증해야 할 설계 sample 수가 많다. 이 기법은 매우 많은 설계사례에서 결과적으론 견고한 것으로 입증되었지만, 분석될 설계의 수가 많으므로 시간과 경비가 많이 소요된다.
선택된 geometry에 대한 입력 값과 출력 값 사이의 선형 회귀(linear regression) 과정에 반응 표면 법(response surface method)으로 대체 모델(surrogate model)을 선정하고, 다목적 유전자 최적 법(MOGA)을 사용하여 펌프 수차 시스템을 최적화한다. 이 최적화 방법 성공의 열쇠는 정확한 대체모델 구축이다.
상기한 종래의 최적화 작업의 최대 문제점은 최적해 군(potential samples)의 case마다 전부 CFD로 검증을 하므로 계산 시간이 방대하고 그로 인해 경비가 많이 소요된다는 것이다.
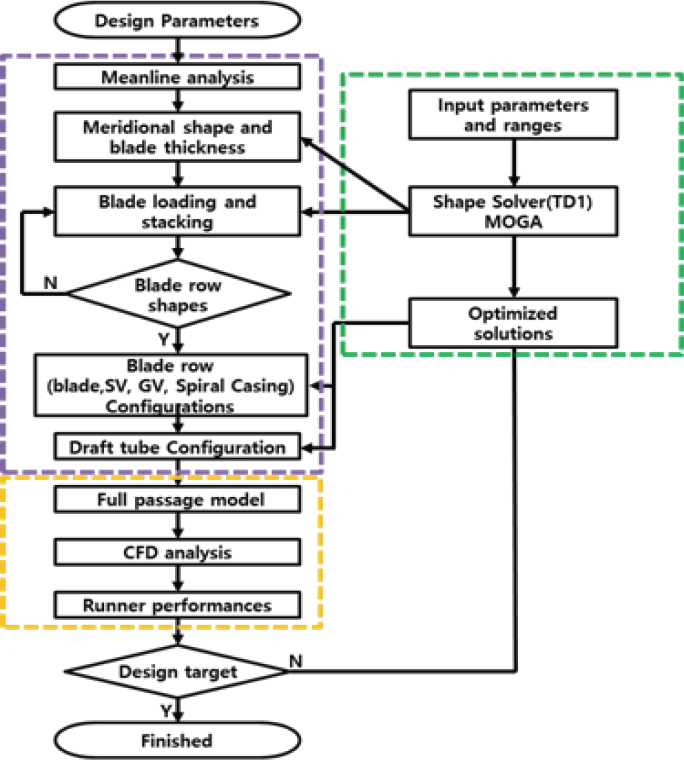
이러한 결점을 극복하고 좀 더 글로벌 최적 솔루션에 확실히 도달하기 위하여 본 연구에서는 Fig. 11처럼 3차원 역해법 solver에서 직접 최적화하는 직접 최적화 법을 사용하였다.
일반적인 직접 최적화 법은 600∼1600개의 설계가 검증, 분석되어야 하므로 많은 시간과 경비가 필요하다. 더구나 CFD와 결합한다는 것은 불가능에 가깝다.
따라서 출력 성능변수와 강한 상관관계가 있는 역해법 solver에 있는 변수(blade loading distribution)와 자오면 파라미터들, Table 4 참조)를 이용하여 흐름의 특성을 직접 조정한다.
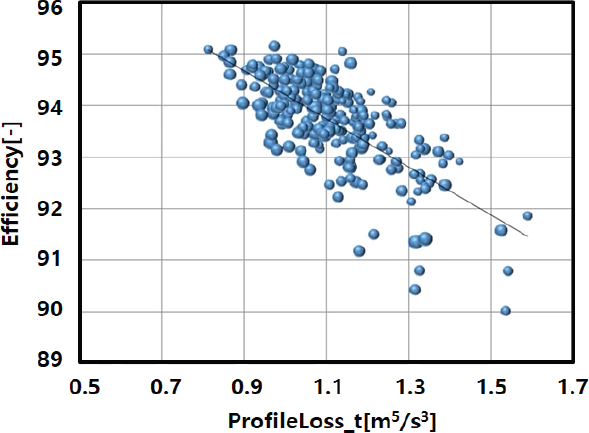
예를 들면 효율과 형상 마찰 손실(Profile loss)의 상관관계(correlation)를 Fig. 12에 나타내었다.
형상 마찰 손실을 줄이면 러너의 효율이 상승한다는 것을 볼 수 있다. 직접 최적화는 이런 상관관계를 이용해서 역해법 solver(TD1)에서 최적화 optimizes를 direct control 할 수 있다.
또한, 이차 흐름(secondary flow) 손실과 효율도 좋은 상관관계를 보이고, 최저 정압(Pmin)도 캐비테이션 억제에 좋은 상관관계를 보여주는 파라미터이다.
본 펌프 수차 시스템 경우, 직접 최적화의 계산 시간은 약 2시간 정도 소요된다. 기존의 최적화 방식대로 메타(meta) 모델 베이스를 최적화하는 데에 비하여 시간이 거의 1/10 수준이다.
전술한 바와 같이 본 연구에서는 직접 최적화로 많은 계산 시간 단축을 달성하였다.
최적화의 설계 툴(tool)은 상업용 소프트웨어인 ADT사의 Turbodesign Optima를 사용하였다.(4) 설계 사양의 검증을 위한 전산 유체(CFD) 계산은 Ansys CFX(2024 R2 version)를 사용하였다.(5)
러너 블레이드 최적 해를 얻기 위한 다목적 유전자 알고리즘(MOGA)에서 목적함수(효율과 캐비테이션)와 제한 조건은 다음과 같다.
| (8) |
여기서, X: 블레이드 로딩 파라미터 공간, Y: 수차 러너 블레이드의 수력학적 효율(50% profile loss & 50% secondary flow factor) 및 정압(Pmin)
본 연구에서는 사용된 MOGA는 Table 5와 같다.
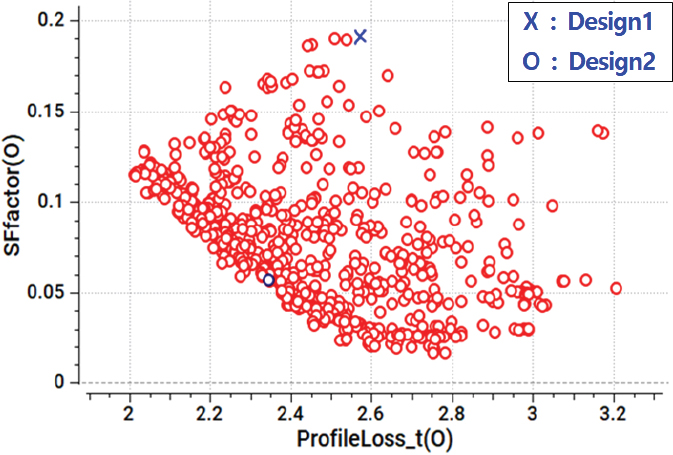
최적화 과정의 파레토 최적해(Pareto solution)에 대한 도식은 Fig. 13에 도시하였다.
그림에서 빨간색 원은 최적화에서 모든 실행 가능한 솔루션을 나타낸다. 최적화에서 탐색한 900개의 설계 중 지정된 제약 조건을 충족하는 모든 솔루션을 실행 가능한 솔루션이라고 한다.
설계 하나하나가 목적함수에 대한 sample 값으로 단계별 진화로 파레토 프런트(Pareto front)에 대한 접근하는 양상을 관찰할 수가 있다.
Fig. 13에서 좌표축의 ProfileLoss_t 목적함수는 전체 프로 파일 손실(total profile loss)의 줄임말로, profile 점도로 인한 유체 마찰 손실의 척도로 사용된다. 이것을 최소화하면 효율성이 향상된다.
SF factor는 이차 흐름 팩터(secondary flow factor)의 줄임말로서, 이는 역 압력 구배 때문에 블레이드 경계층에서 발생하는 이차 유동의 척도이다. 더 높은 이차 흐름은 더 큰 유량 불균일성을 초래하여 손실이 더 커지기 때문에 이차 유동을 최소화하면 효율성이 향상된다.
이처럼 두 목적함수(ProfileLoss_t, SF factor)의 귀결은 효율 향상이다.
Fig. 13에서처럼 빨간색 작은 원은 최적화에서 모든 실행 가능한 솔루션을 나타낸다. 최적화에서 탐색한 900개의 설계 중 지정된 제약 조건을 충족하는 모든 솔루션을 실행 가능한 솔루션이라고 한다.
실현 가능한 해의 앞쪽에 있는 모든 점은 최적해/파레토 해이다. 선택한 점(파란색 원)은 파레토 해 중 하나인데, 최소 정압(Pmin) 조건을 만족하는 sample(blue circle)을 Design2로 선정하였다.
2.5 최적화된 1 MW 펌프 터빈 시스템 형상
펌프 터빈 시스템에서 가장 중요한 부품은 runner blade이다. 최적화 과장은 러너 블레이드 중심으로 설명하고자 한다.
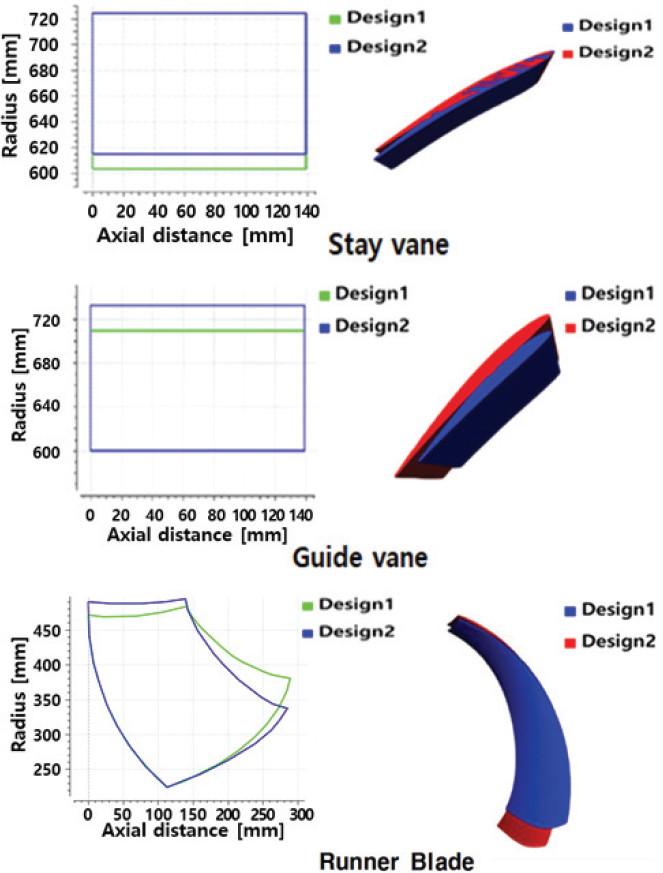
러너 블레이드 최적화 설계가 끝나면 그에 매칭 되게 스테이 베인, 가이드 베인 최적 설계가 진행된다. 최종적으로 얻은 러너 blade row(러너 블레이드, 스테이 베인, 가이드 베인 포함)의 자오면 과 3차원 형상 비교를 Fig. 14와 같이 도시하였다.
Fig. 14에서처럼 최적화된 블레이드(Design 2)의 자오면은 베이스라인 설계 블레이드(Design 1) 자오면 보다 펌프 모드 시 펌프 흡입력을 높여서 결과적으로 성능향상을 목적으로 반경은 좀 더 커졌지만, 후연(trailing edge) 부의 높이는 낮아졌다는 것을 알 수 있다. 3차원 형상은 자오면 변화에 따라 최적화된 형상(Design2)이 길이는 베이스라인 형상(Design1) 보다 길어졌지만, 후연부의 폭은 다소 좁아졌다는 것을 확인할 수 있다.
블레이드 최적화로 인한 블레이드 형상 변화로 그와 매칭되게 스테이 베인과 가이드 베인의 자오면과 3차원 형상도 Fig. 14처럼 재설계 되었다.
스테이 베인은 베이스라인 설계보다 자오면 길이가 미세하게 짧아졌지만 3차원 형상의 큰 변화는 보이질 않는다. 반면에 가이드 베인은 Design1에 비해서 자오면과 3차원 형상이 더 커졌다는 것을 볼 수 있다. 이것은 펌프 모드 성능향상, 즉 양정 확보와 고효율에 집중하다 보니 블레이드에 인접한 가이드 베인의 형상은 블레이드의 매칭 때문에 영향을 받아 커졌고, 스테이 베인은 흐름의 저항을 줄이는 차원으로 작아진 것으로 판단된다.
블레이드 최적화 시 상기 Fig. 14처럼 역해법 설계 solver(상업용 TD1)에서 MOGA Optimizer를 직접 최적화하여 합리적 시간 내에 파레토 최적값을 얻었다. 파레토 최적해 중에서 캐비테이션 발생 변수인 최저 정압(Pmin) 값을 만족하는 최적 해를 어떻게 합리적인 시간 내에 도출하는 것이 중요하다.
이러한 형상 변화로 펌프 입구에 압력이 높아져 흡입력이 더욱 강해져서 흐름이 러너 블레이드가 회전하면서 원심력으로 인해 가속됨으로써 만족할 만한 양정을 확보하여 전체 유동 장이 안정되고 흐름의 불안정성이 발생하지 않는 것으로 판단된다. 이처럼 안정적인 물의 유동이 러너 블레이드, 가이드 베인, 그리고 스테이 베인으로 자연스럽게 흘려 전 수두 손실이 감소되어 효율이 상승하고 시스템이 안정화 된 것으로 판단된다.
터빈 모드시 최적화된 러너 블레이드(Design 2)를 검증하기 위해 정격조건의 베이스라인 설계(Design 1)표면의 비점성 흐름의 압력분포를 Fig. 15에 비교하였다. 이것은 CFD가 필요 없이 역해법 솔버로 바로 취할 수 있는 데이터이기 때문에 간단하게 성능을 검증할 수 있는 좋은 방법이다.
베이스라인 설계(Design1)에 블레이드 표면 압력분포에서 나타났던 쉬라우드(shroud) 후연에서의 음압이 최적화된 러너(Design2)에서는 발생하지 않았다는 것을 알 수 있다. 최적화된 블레이드에서는 캐비테이션에 가장 취약한 후연 쉬라우드 부근에서 최적화된 러너 블레이드를 통해 흐름이 원활하게 흘러가고 있다는 것을 알 수 있다.
이 결과로부터 최적화된 형상은 설계 목표치(정격조건일 때 No cavitation)에 적합하다고 판단해서 본격적인 최적화된 형상의 검증을 CFD로 진행하였다.
3. 수치 해석 및 결과 분석
3.1 수치해석용 격자 시스템 및 경계 조건
본 연구에서 개발한 1MW급 양수발전용 펌프 수차에 대해서 상용 유동 해석 프로그램인 Ansys CFX 2024-R2를 이용하여 성능검증을 위한 수치 해석을 수행하였다.(7)
수치 해석용 성능 예측에 주요한 영향을 미치는 격자는 유체 영역의 기하학적 형상에 적합한 계산 격자 및 해석의 경제성을 고려하여야 한다.
본 연구에서는 정격 조건일 때 레이놀즈(Reynolds) 수가 22.286E6으로 고 레이놀즈수에 해당되고 레이놀즈수가 커지면 경계층 두께가 얇아지므로 격자를 보다 벽 가까이 분포시켜야 한다.
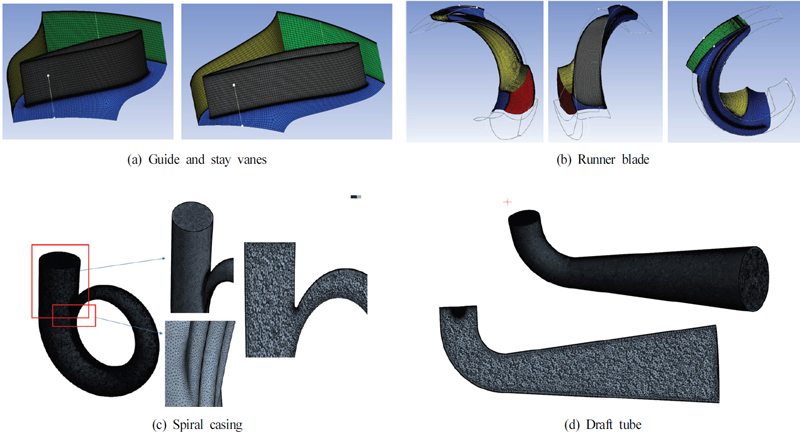
격자 시스템을 Fig. 16처럼 계산 효율을 높이기 위하여 일반적인 계산 격자 생성처럼 유동 상태가 복잡한 blade row의 격자 계를 스파이럴 케이싱, 흡출관보다도 mesh density를 높게 설정하였다. 블레이드 열(blade row) 격자에는 육면체 격자(Hexahedral mesh)로 경계층 첫 번째 grid cell 높이는 0.01mm로 하였고, 엔시스 터보 그리드(Ansys Turbogrid) 기능을 사용하였다.
스파이럴 케이싱 과 흡출관은 사면체 격자(Tetrahedral grid)와 15개의 프리즘 격자 층(Prism grid layer)의 조합으로 작성되었으며, 첫 번째 grid cell 높이는 0.02mm로 하였고, 엔시스 워커 벤치(Ansys Workbench) 플랫폼을 사용하였다.(7)
스파이럴 케이싱의 분기 부분, 흡출관 입구, 벽면 근처에는 아주 조밀하게 구성하고, 점성 영향이 적은 공간에는 상대적으로 더 크게 생성하였다.
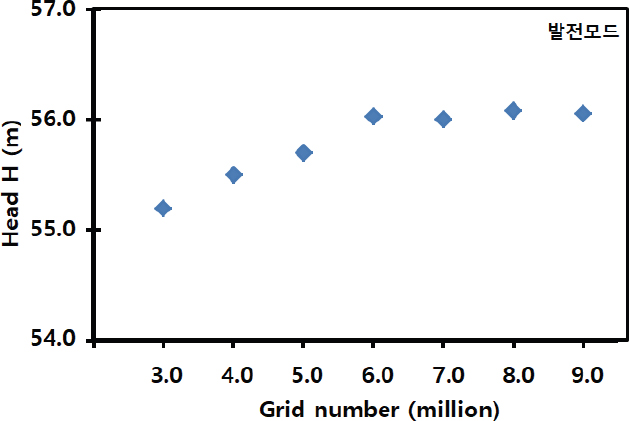
격자 수는 CFD 계산의 정도와 시간에 매우 중요하다. 격자 수가 유동 장에 미치는 영향을 조사하기 위하여 본격적인 CFD 계산을 수행 전에 발전 모드의 정격조건에서 계산 격자수를 변화시켜 가면서 그에 따른 수두 변화에 대한 수치 실험을 수행하였다. 계산 격자의 변화에 따른 수두 변화를 Fig. 17에 도시하였다.
Fig. 17에서처럼 격자 수가 6백만 개에서 수두 변화가 안정화 되고 이상의 격자 수에서는 수두 변화가 1% 미만이었기 때문에 계산 시간 및 비용을 고려하여 격자 수 6백만을 최종 CFD 격자 수로 결정하였다.
계산영역에서의 전체 격자 수는 Table 6과 같다.
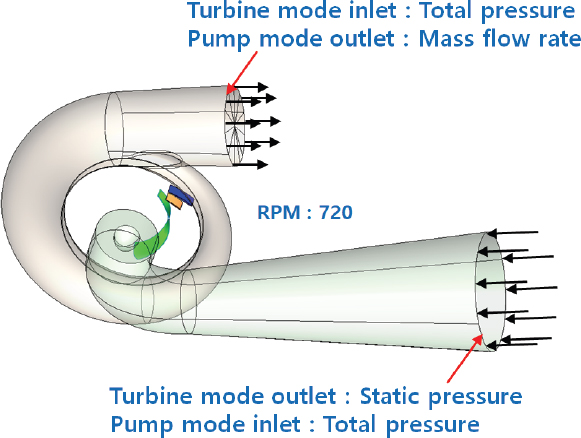
설계 형상을 검증하기 위한 전체 유동 장과 경계조건은 Fig. 18과 같다.
Fig. 18에서처럼 경계조건으로, 펌프 수차의 스파이럴 케이싱 과 흡출관이 펌프와 발전 모드에 대해서 각각 입구 경계조건과 출구 경계조건으로 주어졌다. 발전 모드인 경우, 시스템의 입구와 출구는 각각 전압조건과 정압조건을 부여하였다. 펌프 모드의 입구는 실증 설치 장소의 설계를 바탕으로 전압조건을, 출구는 수치계산의 결과를 바탕으로 질량 유량 조건을 부여하였다.
모든 계산영역에서 벽에는 No-slip condition을 사용하였다. 난류 운동에너지와 난류 소산 빈도를 계산하는데 standard wall function이 사용되었다.
시스템 전체 유동장의 지배 방정식으로 레이놀즈 평균화된 나비에-스토크스 방정식(Steady Reynolds averaged Navier-Stokes equation: Steady RANS)을 CFX solver 기능을 사용하여 해석하였다. 결과 분석은 CFX-post를 사용하였다. 난류 흐름을 모사하기 위해서 회전 유체기계 해석에서 신뢰성을 검증받았던 Shear stress transport(SST) 모델을 사용하였다. 캐비테이션이 발생하고 있는 영역을 VOF (volume of fluid)법 과 버블의 성장, 붕괴를 모사할 수 있는 레일리-플레셋(Rayleigh-Plesset) 모델을 사용하였다(7).
작동 유체는 25∘C 물과 증기로 하였다. Fig. 18에서처럼 Blade row는 단일 통로 모델링으로 회전 주기 옵션(rotational periodicity option)을 사용했다.
수치 해석 시 회전자와 고정자 사이의 경계면 조건은 경계면을 통해 원주 방향으로 평균 된 유동 값을 입력하는 stage interface 방식을 사용하였다.
펌프 터빈 시스템의 입구와 출구 경계조건은 Table 7에 구체적으로 표시하였다.
캐비테이션의 평균 직경 및 포화압력은 각각 2.0×10–6m, 3,169.9 Pa로 설정하였다.
96개 코어 클러스터의 Workstation으로 단일 운영 지점을 시뮬레이션하는데 약 32분 소요되었다.
3.2 구조 해석(Structural analysis)
물의 유동으로 인해 야기되는 펌프 수차 시스템에 대해 외부 응력에 가장 취약한 러너를 중심으로 러너와 구조물에 가해질 수 있는 응력 상태 해석을 통해 펌프 터빈 구조물의 안정성을 검증하기 위해 유한 요소 해석을 Fig. 19과 같이 60만 개의 격자 계에 수치계산으로 도출된 압력 값을 블레이드, 허브(hub), 쉬라우드(shroud)의 부하 값으로 설정하여 유한 요소 해석을 수행하였다.
복합 응력 상태에서 항복을 예측하기 위해 사용되는 주요한 응력 지표들을 계산하였다.
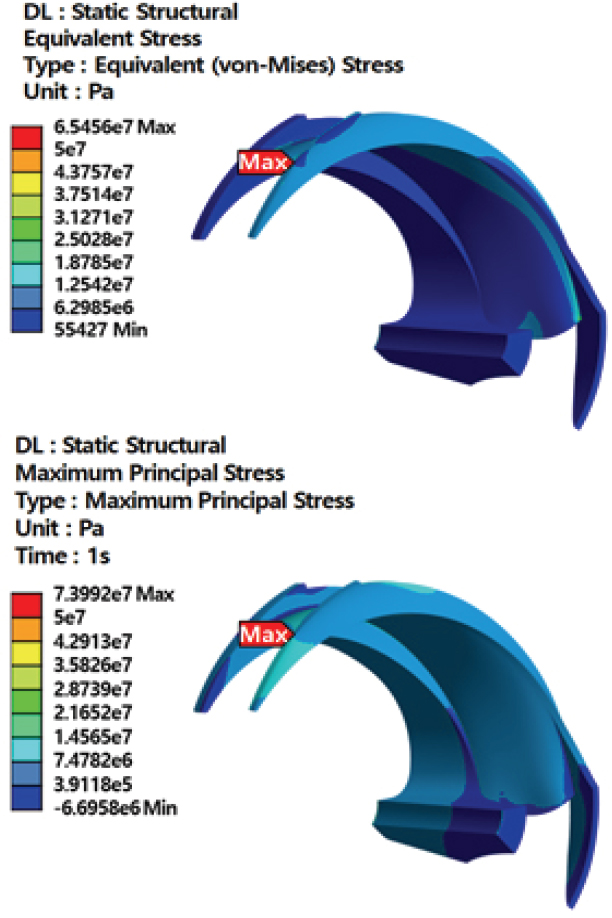
계산 결과 최대 응력 값은 터빈 모드 경우가 중력 가속도와 원심력의 영향으로 펌프 모드보다도 더 큰 응력 값을 가진다는 것을 확인하였고, 터빈 모드 경우, 가장 정확하게 물체의 파괴를 예측하는 기준으로 평가받고 있는 폰 미세스(Von Mises) 응력(최대 비틀림 에너지) 분포와 주응력(Principal stress) 분포를 Fig. 20에 나타내었다.
그림에서처럼 최대 응력 값은 전연의 쉬라우드 부근(Max 표시 부분)에서 발생하였고 폰 미세스 응력은 65 MPa, 주응력의 최댓값은 70MPa 로서 블레이드와 러너 구조물의 재질 SCS 6의 항복 응력 550 MPa에 비해 안전 율(safety factor) 8 이상으로 구조적으로 안전하다고 판단된다.
4. 결과 및 고찰
최적화된 시스템(Design 2)과 베이스라인 시스템(Design 1)의 최적 설계 점에서의 성능 비교를 Table 8에 표시하였다.
최적화 결과, Design2의 터빈 모드에서는 GV 개도 각이 Design1에 비해서(1.15도) 다르게 4.7도 일 때 최고효율 점(Best Efficient Point: BEP)을 나타냈다. 이것은 최적화 과정에서 러너 블레이드의 최적 형상과 matching 하면서 GV sizing이 커졌기 때문이라 판단된다.
베이스라인 결과와 비교해서 최적화된 시스템의 터빈 모드 최고효율은 조금 떨어졌지만, 부분 부하에서의 효율은 상승했다.
펌프 모드의 성능이 상당히 개선된 것을 알 수 있다. 특히 흡출관 수두 손실이 흡출관의 설계개선으로 흡출관에서의 흐름이 개선되어 재순환(recirculation) 영역이 사라져 블레이드로 흡입되는 흐름이 블레이드 면을 따라서 자연스럽게 흡입되어 가이드 베인 및 스테이 베인 사이도 간섭 현상은 보이지 않았다.
러너를 떠난 유동은 가이드 베인 및 스테이 베인의 배압 면(suction surface: ss)에서의 박리 현상도 없이 자연스럽게 흘러 스테이 베인 헤드 손실도 많이 개선된 것을 볼 수 있다. 펌프 수차 최적화로 각 부분에서의 흐름의 불안정성이 해소되어 펌프 모드의 최고효율이 8.92% 향상되었다.
터빈 모드에서는 최적화된 Design2의 최고 효율(91.4%)이 Design1(91.8)보다 0.4% 하락하였지만 유동장에 큰 영향은 없다.
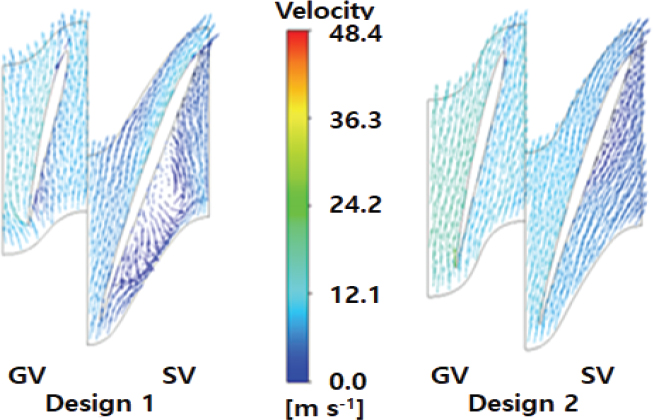
수치 해석 결과, 터빈 모드, 정격조건일 때 블레이드 중간 부분(mid span)에서의 속도 벡터 비교를 Fig. 21에 표시하였다. 터빈 모드인 경우, 정격 조건일 때는 전체적인 흐름의 특성이 유사하다는 것을 알 수 있다. 정격일 때는 베이스라인 설계나 최적화된 설계 모두 흐름에 영향을 끼칠 수 있는 파라미터 변화가 없다는 의미이다.
베이스라인 설계(Design 1) 와 최적화 설계(Design 2) 모두 스테이 베인, 가이드 베인, 그리고 블레이드 표면을 따라 큰 흐름의 불안정이 보이지 않고 원활한 흐름 상태를 보여주고 있다.
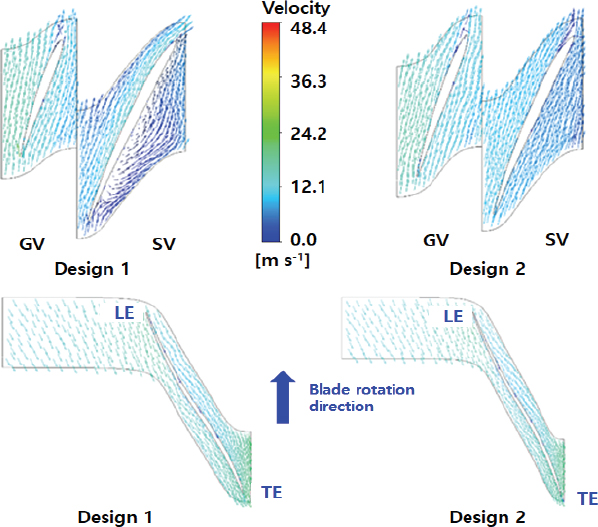
펌프 모드(High flow rate Q=1.5 m3/s)인 경우, 속도 벡터를 Fig. 22에 비교하였다.
그림에서처럼 베이스라인 디자인에서는 스테이 베인 상에서 박리가 발생하고 있지만, 최적화 디자인에서는 부드럽게 유동하고 있는 것을 확인할 수 있다.
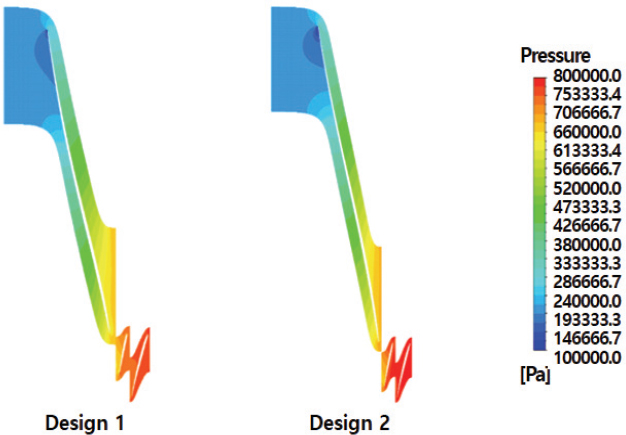
같은 면에서의 압력분포를 Fig. 23에 나타내었다. 최적화된 시스템의 스테이 베인 출구 압력이 베이스라인 시스템의 압력보다 더 높게 나타난다는 것을 알 수 있다. 이것은 러너 블레이드에서부터 흐름 성능이 개선되어서 최종단(final stage)인 스테이 베인에서의 속도가 늦어지면서 압력이 높아져 좀 더 높은 양정을 달성할 수 있다고 하겠다.
최적화된 시스템의 스테이 베인 출구 압력이 베이스라인 시스템의 압력보다 더 높게 나타난다는 것을 알 수 있다. 성능이 개선되어서 높은 양정을 달성할 수 있다고 하겠다.
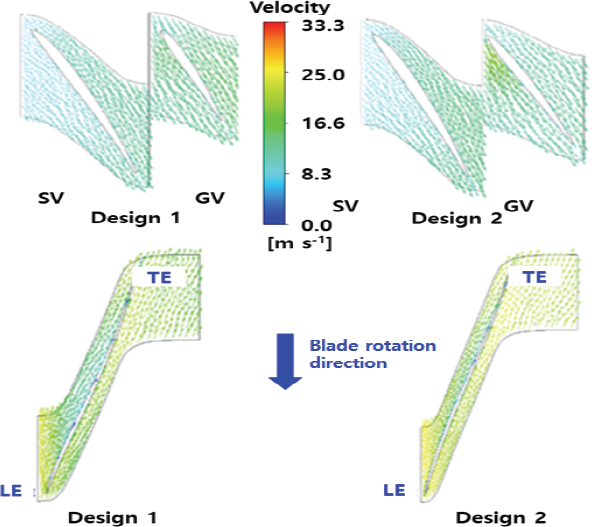
펌프 모드의 유량이 가장 적은 (Flow rate Q=1.1 m3/s)경우, 설계에 따라서 변화가 가장 심한 가이드 베인 과 스테이 베인의 속도 벡터 비교를 Fig. 24에 나타내었다.
한계 유량일 때와 거의 비슷하게 베이스라인 설계의 경우 펌프의 최종 토출 블레이드 열의 최종 단계인 스테이 베인에서 심한 박리 현상이 발생하고 있다는 것을 확인할 수 있다. 이것은 러너 블레이드에서의 미세한 흐름의 불안정성이 가이드 베인을 거치면서 확대되어 최종 단계인 스테이 베인에서는 심한 역 구배 흐름과 박리 현상이 발생 된다고 생각된다. 이에 반하여 최적화된 시스템에서는 가이드 베인 그리고 스테이 베인의 흐름이 원활하게 잘 흘러간다는 것을 볼 수 있다.
베이스라인 설계 때, 펌프 모드의 경우, 흐름이 안정성이 떨어지는 부분부하의 경우 흐름이 박리(separation) 되어 전체 유동장의 안정성과 효율을 떨어지게 하는 것이다.
시스템 전체의 흐름 상태를 확인하기 위하여 펌프 모드인 경우 시스템의 유선 상태를 Fig. 25에 비교하였다.
그림에서처럼 Design 1에서는 흡출관 과 유체의 입구 각이 차이가 나서 선회류(swirl flow)에 의한 재순환 영역(recirculation zone)이 보이지만, 최적화된 Design 2에서는 아무런 소용돌이 없이 자연스럽게 흘러간다는 것을 볼 수 있다.
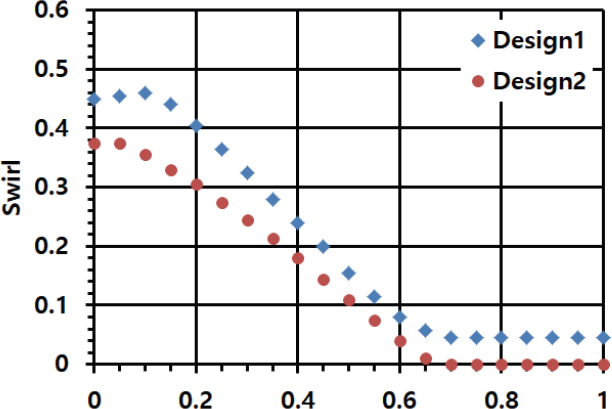
흡출관 입구의 상태를 규명하기 위하여 블레이드 입구에서 하류(흡출관 입구)에서의 선회 류(swirl) 분포를 Fig. 26에 도시하였다. 블레이드에서의 swirl 강도(무차원)는 다음과 같이 정의된다.
| (9) |
여기서, r : radius, Cu : 유동의 점선 방향 속도, rbt : 블레이드 tip 반경, Ubt : 블레이드 tip 속도
블레이드 입구에서부터 swirl 강도는 Design2의 경우가 Design1 보다도 약하고 출구에서도 No swirl 흐름으로 흡출관으로 빠져나가는 것을 알 수 있다(Fig. 25 참조).
유체기계 분야에서 가장 중요한 부분 중의 하나가 캐비테이션을 어떻게 억제하는가이다. 특히 펌프 모드에서 운전 점 이외의 부하일 때 압력이 국부적으로 유체의 증기 압력까지 떨어지는 구역에서 증기 기포가 발생해서 붕괴되는 현상이다. 블레이드 표면이나 벽에 기포의 발생빈도가 높아지면 일정하게 유체를 밀던 힘이 기포 와 부딪히면서 힘에 변화가 생길 수 있어 진동, 소음 그리고 침식 등 여러 가지 나쁜 형상을 일으키기 때문에 설계 시 주의를 요 하는 성능 파라미터이다.
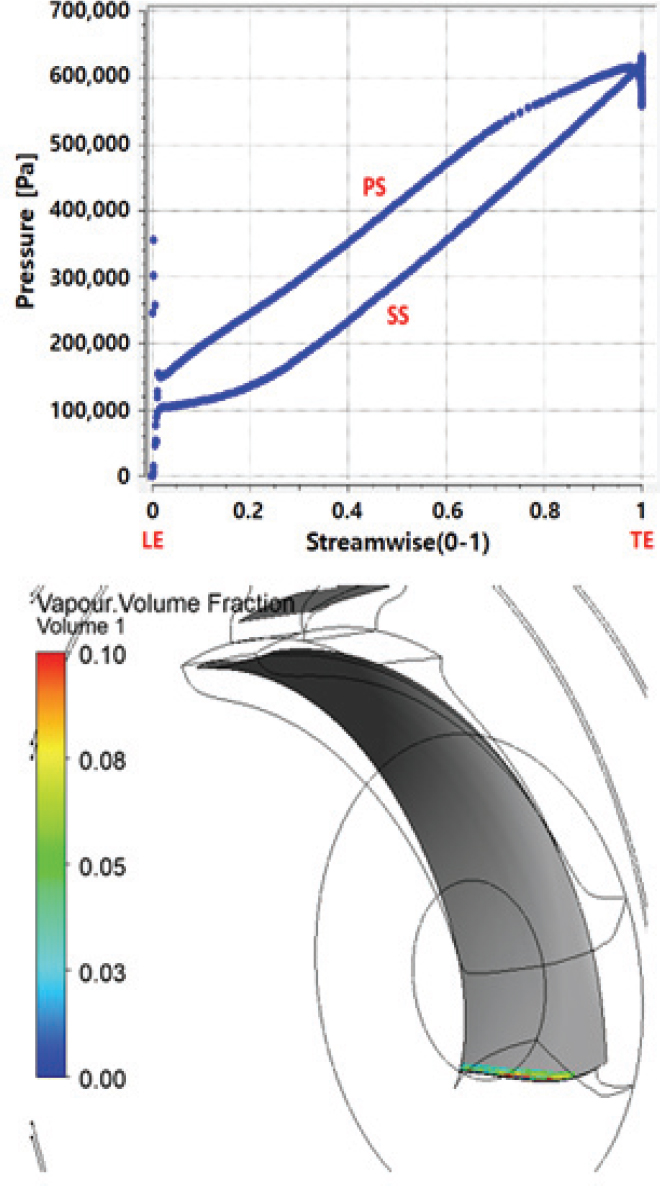
터빈 모드의 80% 부분 부하영역에서의 블레이드 중간영역(mid span)의 압력분포와 증기체적분율(vapour volume fraction) 선도를 Fig. 27에 나타내었다.
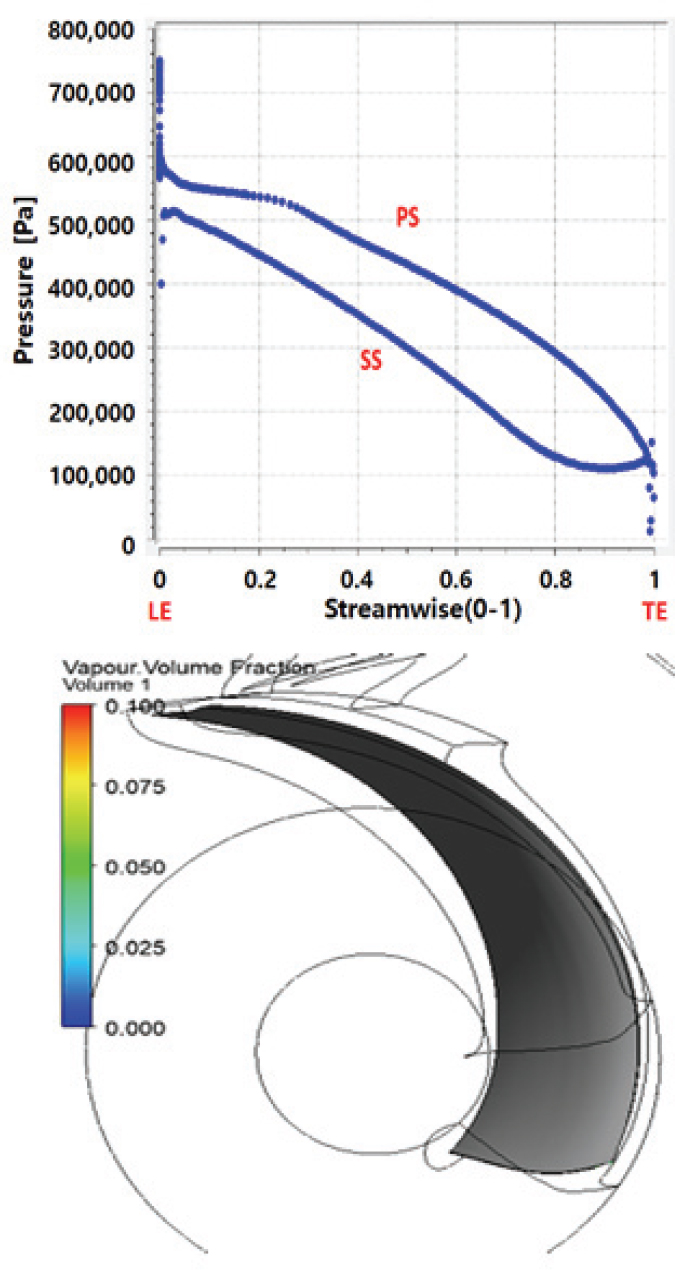
Pressure distribution along the blade surface and vapour volume fraction(turbine mode at the 80% rated flow)
80% 정격 유량일 경우, 블레이드 압력 면과 흡입 면 표면 전체가 설계 점에서 압력분포 행태와 거의 비슷하게 음압이 발생 되지 않을 뿐 아니라 블레이드 면의 증기 체적분율을 보면 블레이드 압력 면보다 상대적으로 압력이 낮은 블레이드 흡입 면에도 기포는 발생하지 않고 있다는 것을 확인할 수 있다.
Fig. 28처럼 최적화된 블레이드에는 베이스라인 블레이드보다 최고효율 점은 약간 손실이 있었지만 유동장 전체가 안정화 되어 있다는 것을 알 수 있다.
펌프 모드의 경우, 가장 적은 유량인 Q=1.1 m3/s의 경우를 Fig. 28에 나타내었다.
블레이드 압력 면과 흡입 면 표면에서 음압은 나타나지 않는다는 것을 알 수 있다. 증기 체적 분율 선도를 보면 전연에서 아주 미세하지만 아주 작은 직경(micro meter 단위)을 가지는 기포가 발생 되고 있다는 것을 확인할 수 있다. 이것은 캐비테이션의 아주 초기 행태로 시스템의 효율 값은 일정하게 유지하고 있지만 좀 더 유량이 하한 유량 이하로 떨어져서 운전하면 국소적으로 압력이 더 떨어져서 블레이드 전연 부근에서 캐비테이션 발생 확률이 높다는 것을 인지할 수 있다. 운전 요주의 하한이라는 것을 판단할 수 있다.
캐비테이션 상태를 평가하기 위해서는 Thoma number(σ)는 IEC 60193에 의거 하여 다음 식으로 표기된다.(8,9)
| (10) |
여기서, NPSH : Net Positive Suction Head(m)
H : 시스템 수두(m)
g : 중력 가속도(m2/s)
ρ : 물의 밀도
PLP : 계산영역의 저압 경계에서 정압(Pa)
Pv : 포화 증기압(Pa)
ALP : 계산영역에서 저압 경계에서 단면적(m2)
먼저 플랜트 시그마(σP)은 0.21로 정격조건에서 수치계산으로 얻은 σ=0.260, 훨씬 안정적인 값을 보여주고 있다.
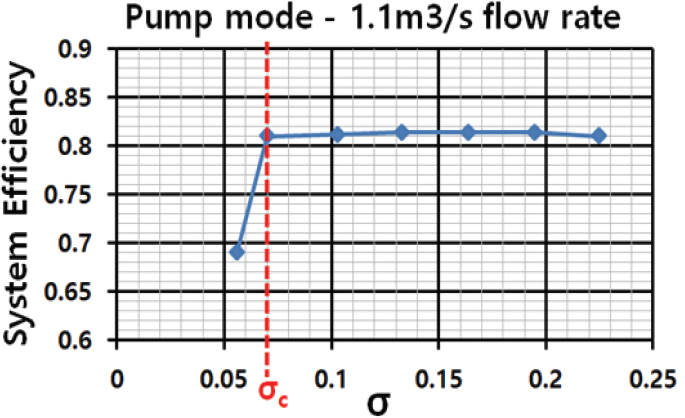
펌프 모드인 경우 유량의 하한값인 Q=1.1 m3/s에서 캐비테이션 특성은 Fig. 29와 같다.
상기 그림에서처럼 캐비테이션 σc=0.07로서 이 값보다 시그마값이 더 적어지면 본격적인 캐비테이션이 발생한다고 평가할 수 있다.
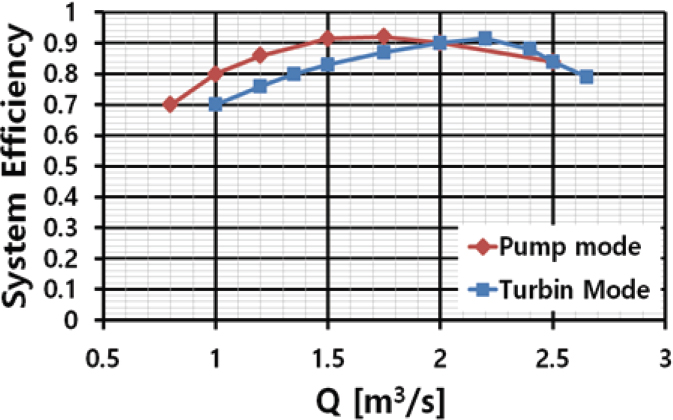
펌프 모드와 발전 모드에 대해서 1 MW 펌프 터빈 시스템의 가장 중요한 성능 지표 중의 하나인 여러 가지 부하에 대한 효율 특성을 Fig. 30에 나타내었다.
발전 및 펌프 모드 최고효율 점(Best efficiency point : BEP)에서 90%를 넘는 고효율을 나타내고 있고 특히 60% 부분 부하에서도 효율이 80%를 유지하고 있다는 것을 알 수 있다. 발전 모드 보다는 펌프 모드 효율이 미세하게 좀 더 높게 나타났다.
양수발전소는 전력계통의 요청에 대규모 에너지를 하루에도 여러 번 짧은 시간 안에 저장(펌핑)하고 방출(발전)해야 하기 때문에 부분 부하변동에도 고효율을 유지하는 것이 대단히 중요하다.
일반적으로 수력기계는 대형일수록 고효율을 나타낸다. 현재 운용 중인 국내 대형(200MW 이상) 양수발전소의 평균 효율이 70%∼85% 정도인 것에 비하면 본 시스템은 소형(1MW)이지만 굉장히 고성능 시스템이라는 것을 알 수 있다.(1)
에너지 저장용 소규모 양수발전에서는 펌프 모드에서의 입력전력이 중요한 성능 인자이다. 그래서 최근에는 좀 더 변동하는 에너지원에 대응하고 그리드의 입력전력을 절약할 수 있는, 가 변속(variable system) 시스템이 선진국에서는 많이 설치되고 있다.
전국에 산재해 있는 7개소의 대형 양수발전소는 전부 고정 속(constant speed)이기 때문에 시스템 현대화 시 고성능 고정속 양수로도 성능개선용으로 소기의 목적을 달성할 수도 있다고 생각된다.
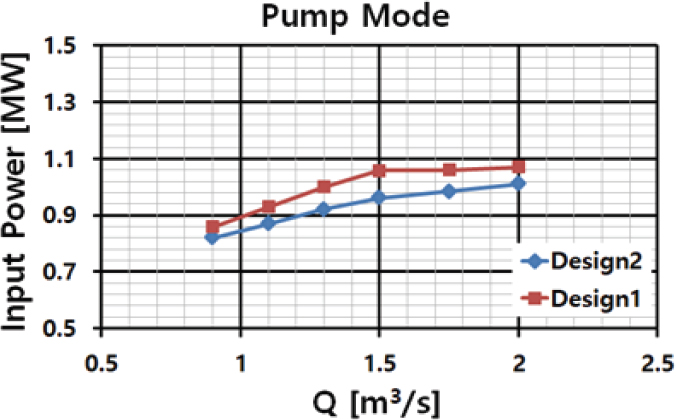
Fig. 31에 베이스라인 시스템 설계 성능과 최적화된 시스템의 부하별 입력전력을 비교하였다.
그림에서처럼 최적화된 펌프 수차에서는 베이스라인 수차보다도 시스템 효율이 개선되어 입력 전압이 적어서 전기를 많이 사용하는 양수 발전소의 펌핑 시 에너지 절약의 한 방안이 될 수 있다는 것을 확인할 수 있다.
5. 결 론
1 MW 급 마이크로 펌프 터빈 시스템을 역해법 설계법과 다목적 최적화 설계 알고리즘을 사용하여 개발한 결과를 요약하면 다음과 같다.
- 1) 본 펌프 터빈 개발에 사용된 직접 최적화 알고리즘은 개발시간 절약과 효율성 측면에서 산업계에 효율적인 최적화 방안이라 사료 된다.
- 2) 본 개발 펌프 터빈 시스템은 정격일 때의 최고효율은 펌프 및 터빈 모드 시 91.2%, 90.5%이며, 60% 부분 부하에서도 효율이 80% 이상을 유지하고 캐비테이션 거동도 보이지 않는 고효율 고성능을 나타냈다.
- 3) 펌프 모드일 때 고효율 시스템으로 인하여 입력전력을 상당히 절약할 수 있다는 것을 확인하였다.
Acknowledgments
본 연구는 2023년도 중소벤처기업부와 한국수력원자력의 재원으로 중소기업기술정보진흥원(TIPA)의 지원을 받아 수행한 연구과제입니다(No.S3395678).
References
- K. H. Ko and Y. H. Jeon, 2018, “New Renewable Energy Output Volatility and the Need for New Pumped-Storage Power Plant Construction”, Water and Future: Journal of Korea Water Resources Association, Vol. 51, pp. 20-24.
-
Jurger Krenn, Helmut Keck, Manfred Sallaberger, 2013, “Small and Mid-Size Pump-Turbines with Variable Speed”, Energy and Power Engineering,Vol. 5, pp. 48-54
[https://doi.org/10.4236/epe.2013.52A007]

-
O.E. Balje, 1962, “A study on design criteria and matching of turbomachines : Part A-similarity relations and design criteria of turbines”, Journal of Engineering for Gas Turbine and Power, 84(1), pp.83-102
[https://doi.org/10.1115/1.3673386]

- Advanced Design Technology, 2022, Turbo Design Suite
- W.Teck Tiow and M. Zangene, 2002, “A novel 3D inverse method for the design of turbomachinery blades in a rotational viscous flow: theory and applications”, Task Quarterly 6, No.1, pp.63-78.
-
Baoshan Zhu, Xuhe Wang, Lei Tan, Dongyue Zhou, Yue Zhao, Shulian Cao, 2015, “Optimization Design of a Reversible Pump-turbine Runner with high Efficiency and Stability “, Renewable Energy,Vol 81, pp. 316-376.
[https://doi.org/10.1016/j.renene.2015.03.050]

- Ansys CFX 2024 R2
-
Singhal,A.K., Athavale M., Li H., and Jiang, Y., 2002, “Mathmatical Basis and Validation of the Full Cavitation Basis and Validation of the Full Cavitation Model, Journal of Fluid Engineering, Vol. 124, pp.617-624
[https://doi.org/10.1115/1.1486223]

-
Janahan Fahlbeck,Hakan Nilson,Mohammad H.Arabnejad, S Salehi, 2024, “Performance characteristics of a contrarotating Pump-turbine in turbine and pump modes under cavitating flow conditions”, Renewable Energy, Vol. 237, pp.1-13.
[https://doi.org/10.1016/j.renene.2024.121605]